In the August 2013 issue of Nature Biotechnology there were two back-to-back methods papers published in the area of network theory:

  1. Baruch Barzel & Albert-László Barabási, Network link prediction by global silencing of indirect correlations, Nature Biotechnology 31(8), 2013, p 720–725. doi:10.1038/nbt.2601.
  2. Soheil Feizi, Daniel Marbach, Muriel Médard & Manolis Kellis, Network deconvolution as a general method to distinguish direct dependencies in networks, Nature Biotechnology 31(8), 2013, p 726–733. doi:10.1038/nbt.2635.

This post is the first of a trilogy (part2, part3) in which my student Nicolas Bray and I tell the story of these papers and why we took the time to read them and critique them. 

We start with the Barzel-Barabási paper that is about the applications of a model proposed by Barzel and his Ph.D. advisor, Ofer Biham (although all last names start with a B, Biham is not to be confused with Barabási):

In order to quantify connectivity in biological networks, Barzel and Biham proposed an experimental perturbation model in the paper Baruch Barzel & Ofer Biham, Quantifying the connectivity of a network: The network correlation function method, Phys. Rev. E 80, 046104 (2009) that forms the basis for network link prediction in Barzel-Barabási. In the context of biology, link prediction refers to the problem of identifying functional links between genes from data that may be confounded by indirect effects. For example, if gene A inhibits the expression of gene B, and also gene B inhibits the expression of gene C, then if the expression of A increases, it will decrease the expression of B, which in turn increase C. Therefore one might observe correlation in the expression levels of gene A and C, even though there is no direct interaction between them. The Barzel-Biham model is based on perturbation experiments. Assuming that a system of genes is in equilibrium, it is a model for the change in expression of one gene in response to a small perturbation in another.

The parameters in the Barzel-Biham model are entries in what they call a “local response matrix” S (any matrix with S_{ii}=0 for all i). Physical arguments pertaining to perturbations at equilibrium lead to the equations

G=SG \, (off the diagonal) and G_{ii}=1 for all i.                                  (1)

for a “global response matrix” G that can, in principle, be observed and used to infer the matrix S. The innovation of Barzel and Barabási is to provide an approximate formula for recovering S from G, specifically the formula

S \approx (G-I+D((G-I)G))^{-1}                                                       (2)

where D(M) denotes the operation setting off-diagonal elements of M to zero. A significant part of the paper is devoted to showing that the approximation (2) is good. Then they suggest that (2) can be used to infer direct causal links in regulatory networks from collections of expression experiments. Barzel and Barabási claim that the approximation formula (2) is necessary because exact inference of S from G requires solving the intractable system of n^2 equations

G=SG \, (off the diagonal) and S_{ii}=0 for all i.                                  (3)

The assertion of intractability is based on the claim that the equations are coupled. They reason that since the naïve matrix inversion algorithm requires O(m^3) operations for m equations, the solution of (3) would require time O(n^6). When we looked at this system, our first thought was that while it is large, it is also structured. We sat down and started examining it by writing down the equations for a simple case: a matrix S for a graph on 3 nodes. We immediately noticed the equations decoupled into n systems of n equations where system i is given by S_{ii}=0 and G_{ij} = \sum_k S_{ik} G_{kj}, \, (j \neq i), with the n unknowns S_{i1},\ldots,S_{in}. This immediately reduces the complexity to O(n^4), or even O(n^3) by simple parallelization. In other words, the system is trivially tractable.

But there is more: while looking at the paper I had to take a quick bathroom break, and by the time I returned Nick had realized he could apply the Sherman-Morrison formula to obtain the following formula for the exact solution:

S=I-D(1/G^{-1})G^{-1}.                                                                    (4)

Here the operator “/” denotes element-wise division, a simple operation to execute, so that inferring S from G requires no more than inverting G and scaling it, a formula that is also much simpler and more efficient to compute than (2). [Added 2/23: Jordan Ellenberg  pointed out the obvious fact that G=SG off the diagonal means that SG=G-D for some diagonal matrix D, and therefore S=I-DG^{-1} and since the diagonal entries of S must be zero it follows that D=D(1/G^{-1}). In other words, the Sherman-Morrison formula is not even needed]. While it would be nice for us to claim that our managing to quickly supersede the main result of a paper published in Nature Biotechnology was due to some sort of genius, in fact the entire exercise would be suitable for an undergraduate linear algebra homework problem. Barabási likes to compare himself to the great physicist and nobel laureate Subrahmanyan Chandrasekhar, but it is difficult to imagine the great Chandrasekhar having similar difficulties.

The approach to solving (4) has an implication that is even more important than the solution itself. It provides a dual formula for computing G from S according to (1), i.e. to simulate from the model. Using the same ideas as above, one finds that

G=TD(1/T) where T=(S-I)^{-1}.                                              (5) 

Unlike Barzel & Barabási that resorted to simulating with Michaelis-Menten dynamics in their study of performance of their approximation, using (4) we can efficiently simulate data directly from the model. One issue with Michaelis-Menten dynamics is that they make more sense for enzymatic networks as opposed to regulatory networks (for more on this see Karlebach, G. & Shamir, R. Modelling and analysis of gene regulatory networks, Nat Rev Mol Cell Biol 9, 770–780 (2008)), but in any case performance on such dynamics is hardly a validation of (2) since its mixing apples and oranges. So what happens when one simulates data from the Barzel-Biham model and then tries to recover the parameters?

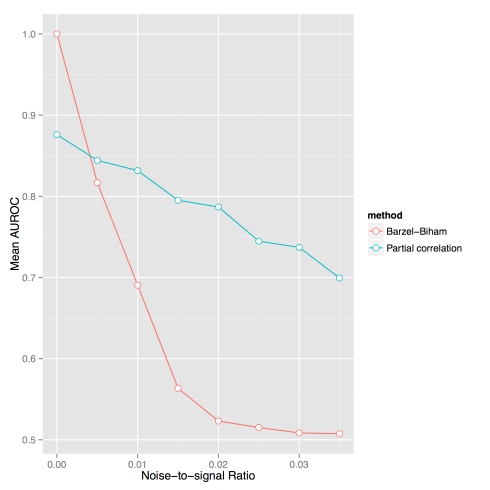
bb_res

A comparison of the standard method of regularized partial correlations with exact inference for the Barzel-Biham model. Random sparse graphs were generated according to the Erdös-Renyi graph model G(5000,p) where p was varied to assess performance at different graph densities (shown on x-axis) The y-axis shows the average AUROC obtained from 75 random trials at each density.

When examining simulations from the Barzel-Biham model with graphs on 5,000 nodes (see Figure above), we were surprised to discover that when adding even small amounts of noise, the exact algorithm (4) failed to recover the local response matrix from G (we also analyzed the approximation (3) and observed that it always resulted in performance inferior to (4), and that 5% of the time the correlation with the exact solution was negative). This sensitivity to noise is due to the term D(1/G^{-1}) in the exact formula which becomes problematic if the diagonal entries of G^{-1} are close to zero.

Some intuition for the behavior of G^{-1} may be gained from noting that if S is such that its geometric sum converges, the diagonal of G^{-1} is equal to that of I+S+S^2+S^3+\cdots. If S has mixed signs and there is significant feedback within the network, the diagonal of G^{-1} may be close to zero and any noise in the measurement of G could create very large fluctuations in the inferred S. This means that the results in Figure 1 are not dependent on the graph model chosen (Erdös-Renyi) and will occur for any reasonable model of gene regulatory networks including the modeling of both enhancers and repressors. From Figure 2a in their paper, it appears that Barzel and Barabási used in their simulation an S with only positive entries that would preclude such effects. Such an assumption is biologically unrealistic.

However, the difficulties with noise for the Barzel-Biham model go much deeper. While a constant signal-to-noise ratio, as assumed by Barzel and Barabasi, is a commonly used model for errors in experiments, it is important to remember that there is no experiment for directly measuring the elements of G. Obtaining G_{ij} from an experiment is done by making a small perturbation of size e to gene i, observing the change in gene j, and then dividing that change by e. This last step increases the noise on the estimate of G_{ij} by a factor of 1/e (a large number, for a perturbative experiment) above the noise already present in the measurements. Increasing e acts to remove the system from the perturbative regime and thereby increases the intrinsic error in estimating G.  It is therefore the case that attaining reasonable error on G will require very low noise in the original measurements. In this case of biological networks this would mean performing many replicates of the experiments. However, as Barzel & Barabási acknowledge in their paper, even a single replicate of a perturbation experiment is not currently feasible.

While the exact algorithm (4) for inverting the Barzel-Biham model performs poorly, we found that a widely used shrinkage method based on partial correlation (Schäfer, J. & Strimmer, K. A Shrinkage Approach to Large-Scale Covariance Matrix Estimation and Implications for Functional Genomics, Statistical Applications in Genetics and Molecular Biology 4, (2005)) outperforms the exact algorithm (blue curve in Figure above). This suggests that there is no input for which (4) might be useful. The method is not even ideal for inference from data generated by the model it is based on.

This brings us to the “results” section of the paper. To demonstrate their method called Silencer, Barzel & Barabási ran it on only one of three datasets from the DREAM5 data. They then compared the performance of Silencer to three out of thirty five methods benchmarked in DREAM5. The Barzel-Biham model is for perturbation experiments, but Barzel & Barabási just threw in data from another universe (e.g. mutual information matrices). But lets just go with that for a moment. Their results are shown in the figure below:

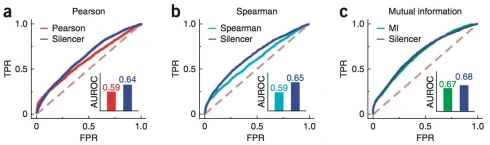
Barzel-Barabasi_Figure

Figure 3 from Barzel-Barabási.

The three methods tested potential improvements on are Pearson, Spearman and Mutual Information. Pearson and Spearman rank 16/35 and 18/35 respectively in the DREAM5 benchmarks. There may be some reason why Silencer applied on top of these methods improves performance: in the case where G is a correlation matrix, the path interpretation given by Barzel and Barabási connects the inference procedure to Seawall Wright’s path coefficients (ca. 1920), which in turn suggests an interpretation in terms of partial correlation. However in the case of mutual information, a method that is ranked 19/35 in the DREAM5 benchmarks, there is no statistically significant improvement at all. The improvement is from an AUROC of 0.67 to 0.68. Amazingly, Barzel and Barabási characterize these results by remarking that they “improve upon the top-performing inference methods” (emphasis on top is ours).  Considering that the best of these rank 16/35 the use of the  word “top” seems, shall we say, unconventional.

We have to ask: how did Barzel & Barabási get to publish a paper in the journal Nature Biotechnology on regulatory network inference without improvement or testing on anything but a handful of mediocre DREAM5 methods from a single dataset? To put the Barzel-Barabási results in context, it is worth considering the standards the Feizi et al. paper were held to. In that paper the authors compared their method to DREAM5 data as well, except they tested on all 3 datasets and 9 methods (and even on a community based method). We think its fair to conclude that significantly more testing would have to be done to argue that Silencer improves on existing methods for biological network inference. 

We therefore don’t see any current practical utility for the Barzel-Biham model, except possibly for perturbation experiments in small sub-networks. Even then, we don’t believe it is practical to perform the number of experiments that would be necessary to overcome signal to noise problems.

Unfortunately the problems in Barzel-Barabási spill over into a follow up article published by the duo: Barzel, Baruch, and Albert-László Barabási, “Universality in Network Dynamics.” Nature Physics 9 (2013). In the paper they assume that the local response matrix S has entries that are all positive, i.e. they do not allow for inhibitory interactions. Such a restriction immediately renders the results of the paper, if they are to be believed, moot in terms of biological significance. Moreover, the restrictions on S appear to be imposed in order to provide approximations to G that are unnecessary in light of (5). Given these immediate issues, we suspect that were we to read the Universality paper carefully, it is quite likely this post would have to be lengthened considerably.

These are not the first of Barabási’s papers to package meaningless and incoherent results in Nature/Science publications. In fact, there is a long history of Barabási publishing with fanfare in top journals only to have others respond by publishing technical comments on his papers, in many cases refuting completely the claims he makes. Unfortunately many of the critiques are not well known because they are rejected from the journals where Barabási is successful, and instead find their way to preprint servers or more specialized publications. Here is a partial list of Barabási finest and the response(s):

  1. Barabasi is famous for the “BA model”, proposed in Barabási and Albert ‘Emergence of Scaling in Random Networks“, Science, Vol. 286 15 October 1999, pp. 509-512. Lada Adamic and Bernardo Huberman immediately refuted the practical applications of the model. Moreover, as pointed out by Willinger, Alderson and Doyle, while it is true that scale-free networks exhibit some interesting mathematical properties (specifically they are resilient to random attack yet vulnerable to worst-case), even the math was not done by Barabási but by the combinatorialists Bollobás and Riordan.
  2. Barabási has has repeatedly claimed metabolic networks as prime examples of scale-free networks, starting with the paper Jeong et al., “The large-scale organization of metabolic networks“, Nature 407 (2000). This fact has been disputed and refuted in the paper Scale Rich Metabolic Networks by Reiko Tanaka.
  3. The issue of attack tolerance was the focus of Error and attack tolerance of complex networks by Réka Albert, Hawoong Jeong & Albert-László Barabási in Nature 406 (2000). John Doyle refuted the paper completely in this paper.
  4. In the paper “The origin of bursts and heavy tails in human dynamics” published in Nature 435 (2005) Barabási pretends to offer insights into the “bursty nature of human behavior” (by analyzing e-mail). In a follow up comment Daniel Stouffer, Dean Malmgren and Luis Amaral demonstrate that the reported power-law distributions are solely an artifact of the analysis of the empirical data and the proposed model is not representative of e-mail communication patterns.
  5. Venturing into the field of control theory, the paper “Controllability of complex networks” by Liu, Slotine and Barabási, Nature 473 (2011) argues that “sparse inhomogeneous networks, which emerge in many real complex systems, are the most difficult to control, but that dense and homogeneous networks can be controlled using a few driver nodes.” Not so. In a beautiful and strong rebuttal, Carl Bergstrom and colleagues show that a single control input applied to the power dominating set is all that is required for structural controllability of most, if not all networks. I have also blogged about this particular paper previously, explaining the Bergstrom result and why it reveals the Barabási paper to be a control theory embarrassment.

In other words, Barabási’s “work” is a regular feature in the journals Nature and Science despite the fact that many eminent scientists keep demonstrating that the network emperor has no clothes.

Post scriptum. After their paper was published, Barzel and Barabási issued a press release claiming that “their research moves the team a step closer in its quest to under­stand, pre­dict, and con­trol human disease.” The advertisment seems like an excellent candidate for Michael Eisen’s pressies.