In this blog post I offer a cash prize for computing a p-value [update June 9th: the winner has been announced!]. For details about the competition you can skip directly to the challenge. But context is important:
Background
I’ve recently been reading a bioRxiv posting by X. Lan and J. Pritchard, Long-term survival of duplicate genes despite absence of subfunctionalized expression (2015) that examines the question of whether gene expression data (from human and mouse tissues) supports a model of duplicate preservation by subfunctionalization.
The term subfunctionalization is a hypothesis for explaining the ubiquity of persistence of gene duplicates in extant genomes. The idea is that gene pairs arising from a duplication event evolve, via neutral mutation, different functions that are distinct from their common ancestral gene, yet together recapitulate the original function. It was introduced in 1999 an alternative to the older hypothesis of neofunctionalization, which posits that novel gene functions arise by virtue of “retention” of one copy of a gene after duplication, while the other copy morphs into a new gene with a new function. Neofunctionalization was first floated as an idea to explain gene duplicates in the context of evolutionary theory by Haldane and Fisher in the 1930s, and was popularized by Ohno in his book Evolution by Gene Duplication published in 1970. The cartoon below helps to understand the difference between the *functionalization hypotheses (adapted from wikipedia):
Lan and Pritchard examine the credibility of the sub- and neofunctionalization hypotheses using modern high-throughput gene expression (RNA-Seq) data: in their own words “Based on theoretical models and previous literature, we expected that–aside from the youngest duplicates–most duplicate pairs would be functionally distinct, and that the primary mechanism for this would be through divergent expression profiles. In particular, the sub- and neofunctionalization models suggest that, for each duplicate gene, there should be at least one tissue where that gene is more highly expressed than its partner.”
What they found was that, in their words, that “surprisingly few duplicate pairs show any evidence of sub-/neofunctionalization of expression.” The went further, stating that “the prevailing model for the evolution of gene duplicates holds that, to survive, duplicates must achieve non-redundant functions, and that this usually occurs by partitioning the expression space. However, we report here that sub-/neofunctionalization of expression occurs extremely slowly, and generally does not happen until the duplicates are separated by genomic rearrangements. Thus, in most cases long-term survival must rely on other factors.” They propose instead that “following duplication the expression levels of a gene pair evolve so that their combined expression matches the optimal level. Subsequently, the relative expression levels of the two genes evolve as a random walk, but do so slowly (33) due to constraint on their combined expression. If expression happens to become asymmetric, this reduces functional constraint on the minor gene. Subsequent accumulation of missense mutations in the minor gene may provide weak selective pressure to eventually eliminate expression of this gene, or may free the minor gene to evolve new functions.”
The Lan and Pritchard paper is the latest in a series of works that examine high-browed evolutionary theories with hard data, and that are finding reality to be far more complicated than the intuitively appealing, yet clearly inadequate, hypotheses of neo- and subfunctionalization. One of the excellent papers in the area is
Dean et al. Pervasive and Persistent Redundancy among Duplicated Genes in Yeast, PLoS Genetics, 2008.
where the authors argue that in yeast “duplicate genes do not often evolve to behave like singleton genes even after very long periods of time.” I mention this paper, from the Petrov lab, because its results are fundamentally at odds with what is arguably the first paper to provide genome-wide evidence for neofunctionalization (also in yeast):
M. Kellis, B.W. Birren and E.S. Lander, Proof and evolutionary analysis of ancient genome duplication in the yeast Saccharomyces cerevisae, Nature 2004.
At the time, the Kellis-Birren-Lander paper was hailed as containing “work that may lead to better understanding of genetic diseases” and in the press release Kellis stated that “understanding the dynamics of genome duplication has implications in understanding disease. In certain types of cancer, for instance, cells have twice as many chromosomes as they should, and there are many other diseases linked to gene dosage and misregulation.” He added that “these processes are not much different from what happened in yeast.” and the author of the press releases added that “whole genome duplication may have allowed other organisms besides yeast to achieve evolutionary innovations in one giant leap instead of baby steps. It may account for up to 80 percent (seen this number before?) of flowering plant species and could explain why fish are the most diverse of all vertebrates.”
This all brings me to:
In the abstract of their paper, Kellis, Birren and Lander wrote that:
“Strikingly, 95% of cases of accelerated evolution involve only one member of a gene pair, providing strong support for a specific model of evolution, and allowing us to distinguish ancestral and derived functions.” [boldface by authors]
In the main text of the paper, the authors expanded on this claim, writing:
“Strikingly, in nearly every case (95%), accelerated evolution was confined to only one of the two paralogues. This strongly supports the model in which one of the paralogues retained an ancestral function while the other, relieved of this selective constraint, was free to evolve more rapidly”.
The word “strikingly” suggests a result that is surprising in its statistical significance with respect to some null model the authors have in mind. The data is as follows:
The authors identified 457 duplicated gene pairs that arose by whole genome duplication (for a total of 914 genes) in yeast. Of the 457 pairs 76 showed accelerated (protein) evolution in S. cerevisiae. The term “accelerated” was defined to relate to amino acid substitution rates in S. cerevisiae, which were required to be 50% faster than those in another yeast species, K. waltii. Of the 76 genes, only four pairs were accelerated in both paralogs. Therefore 72 gene pairs showed acceleration in only one paralog (72/76 = 95%).
So, is it indeed “striking” that “in nearly every case (95%), accelerated evolution was confined to only one of the two praralogues”? Well, the authors don’t provide a p–value in their paper, nor do they propose a null model with respect to which the question makes sense. So I am offering a prize to help crowdsource what should have been an exercise undertaken by the authors, or if not a requirement demanded by the referees. To incentivize people in the right direction,
I will award 
to the person who can best justify a reasonable null model, together with a p-value (p) for the phrase “Strikingly, 95% of cases of accelerated evolution involve only one member of a gene pair” in the abstract of the Kellis-Birren-Lander paper. Notice the smaller the (justifiable) p-value someone can come up with, the larger the prize will be.
Bonus: explain in your own words how you think the paper was accepted to Nature without the authors having to justify their use of the word “strikingly” for a main result of the paper, and in a timeframe consisting of submission on December 17th 2003 (just three days before Hanukkah and one week before Christmas) and acceptance January 19th 2004 (Martin Luther King Jr. day).
Rules
To be eligible for the prize entries must be submitted as comments on this blog post by 11:59pm EST on Sunday May 31st June 7th, 2015 and they must be submitted with a valid e-mail address. I will keep the name (and e-mail address) of the winner anonymous if they wish (this can be ensured by using a pseudonym when submitting the entry as a comment). The prize, if awarded, will go to the person submitting the most complete, best explained solution that has a p–value calculation that is correct according to the model proposed. Preference will be given to submission from students, especially undergraduates, but individuals in any stage of their career, and from anywhere in the world, are encouraged to submit solutions. I reserve the right to interpret the phrase “reasonable null model” in a way that is consistent with its use in the scientific community and I reserve the right to not award the prize if no good/correct solutions are offered. Participants do not have to answer the bonus question to win.
Bits of DNA 
143 comments
Comments feed for this article
May 26, 2015 at 4:24 am
GM
The null model would be that some proportion of genes evolves faster but this has nothing to do with the behavior of the other gene in the pair.
The most simple-minded thing would be to consider
genes, 
of them at random having the property of accelerated divergence. Then under the null model the probability of both members of a pair having that property would be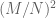 
, and the 
-value is calculated as the binomical cdf for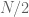 
trials and 
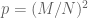. For 
and 
the cdf for up to 4 such successes is 0.7883 It’s also 0.17 for 1, and 0.042 for 0, meaning that even if there wasn’t a single case of both genes in a pair showing acceleration, there still wouldn’t be much that can be really confidently said about the subject from this sample. One expects 3 such pairs by chance.
It probably also matters how many genes show accelerated evolution in the rest of the genome, but I don’t think that was discussed in the paper so I am not considering it either.
May 26, 2015 at 11:48 am
Michael Eisen
M = 80 (72 singles plus two pairs) – not that it really matters
May 26, 2015 at 12:45 pm
GM
You’re correct, my bad.
Then it’s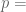
0.7256.
June 5, 2015 at 2:28 pm
Manolis Kellis
Dear GM, thanks for submitting the very first entry 🙂 Our paper was focused on comparing two models of evolution, and the distinct mechanisms by which they would predict that accelerated rates would occur. The null that you’re proposing would correspond to a model of independent evolution, whereby each copy would accelerate randomly, without regard to the function, preservation, or evolutionary rate of the other copy. Even though we did not consider this model in our paper, it would be inconsistent with the highly coordinated pattern of gene loss observed in regions of duplicate synteny, as i describe in my post to Pavel and his students https://liorpachter.wordpress.com/2015/05/26/pachters-p-value-prize/#comment-4436 It would be a fine null if drawing pairs of balls at random, but not a great model of evolution given what know of duplicate preservation. I hope this helps.
June 5, 2015 at 6:48 pm
Joshua Plotkin
Hi Manolis,
Thank you for continuing to reply to these comments.
In several of your posts from today you seem to mis-interpret the “independent acceleration” model that many commentators suggest as a natural null model. The “independent acceleration” model posits, simply, that whether one copy of a retained duplicate gene pair exhibits accelerated evolution is independent of whether its paralogous copy accelerates. This null model does not posit, as you suggest in comments today, that whether one copy is *retained* in the genome is independent of whether the other copy is retained (which clearly makes no evolutionary sense, I agree, and is soundly rejected by the data).
Your posts from today also identify an essential difference between the commonplace interpretation of the “Ohno” model, as summarized by Force et al (1999), versus the interpretation used in KBL 2004. Ohno (1970) is of course a very large book, and so Lynch and Force (1999, 2000) were careful to define what they meant by the shorthand term “classic” or “Ohno” model:
Force el all 1999 (KBL Ref 21): “Under the classical model for the evolution of duplicate genes, one member of the duplicated pair usually degenerates within a few million years by accumulating deleterious mutations, while the other duplicate retains the original function. This model further predicts that on rare occasions, one duplicate may acquire a new adaptive function, resulting in the preservation of both members of the pair, one with the new function and the other retaining the old.”
Lynch & Force 2000 (KBL Ref 20): “It has often been argued that gene-duplication events are most commonly followed by a mutational event that silences one member of the pair, while on rare occasions both members of the pair are preserved as one acquires a mutation with a beneficial function and the other retains the original function. …. An alternative hypothesis is that gene duplicates are frequently preserved by sub-functionalization, whereby both members of a pair experience degenerative mutations that reduce their joint levels and patterns of activity to that of the single ancestral gene.”
In other words, as you have pointed out today, Lynch and Force use the term “Ohno” or “classical” to mean strict neo-functionalization: a model in which the preservation of duplicated genes requires exactly one copy to acquire a new function. Insofar as neo-functionalization can be assessed by studying evolutionary rates at all, therefore, the classical model summarized by Force et al (and cited by KBL) posits that exactly one paralogous copy will exhibit acceleration within every retained duplicated pair. The KBL data clearly reject this classical model, instead of supporting it.
Of course you’re right that, in fact, Ohno’s 1970 book contains lots of various ideas for the preservation of duplicated genes — including even the sub-functionalization idea that has since come to be associated with Force et al. Many of Ohno’s possible explanations do suggest that at least one paralogous copy will change its evolutionary rate (because changes in mRNA expression levels induce rate changes).
In any case, the bottom line is that evolutionary biologists have long come to associate the classical Ohno model with strict neo-functionalization, exactly as summarized by Force et al (1999). And so, when readers of the KBL paper see citation to Force et al 1999 and read the conclusion that the KBL analysis provides “strong support for a specific model of evolution” or allow you “to distinguish ancestral and derived functions” they naturally assume that you mean the analysis supports neo-functionalzation (as opposed to supporting just anything Ohno said in his entire 1970 book). But the data do not seem to support neo-functionalzation at all. Hence the confusion of some KBL readers, on this point.
May 26, 2015 at 5:55 am
oz
Consider $2n$ elements divided into $n$ distinct pairs. Suppose that we choose at random uniformly and without replacement
$k$ out of the $2n$ elements. We count the number of pairs $r$ for which {\bf both} elements of the pair were chosen.
We next compute the probability to observe at most $r$ such pairs.
Let $X$ be the random variable counting the number of such pairs. Then, the probability of getting $X=0$, i.e. all $k$ elements are chosen from $k$ distinct pairs, is given by (assuming $k \leq n$):
$$
P(X=0) = \frac{\binom{n}{k} 2^k}{\binom{2n}{k}}
$$
More generally, the probability of observing exactly $i$ such pairs, is given by (for $i=0,..,\lfloor \frac{k}{2} \rfloor$):
$$
P(X=i) = \frac{\binom{n}{i} \binom{n-i}{k-2i} 2^{k-2i}}{\binom{2n}{k}}
$$
Explanation: the total number of possibilities of choosing $k$ out of $2n$ elements is in the denominator.
In the numerator, we have to choose the pairs for which both elements were chosen ($i$ such pairs). Then, we need to choose
out of the remaining $n-i$ pairs, ,the $k-2i$ pairs for which exactly one element was chosen, and then, for each of these pairs,
we need to decide which of the two elements in the pair was chosen. This gives the numerator.
The p-value is given by:
$$
p_{n,k,r} \equiv P(X \leq r) = \sum_{i=0}^r P(X=i)
$$
Setting $n=457$ gene pairs, $k=80$ genes ($72$ pairs with one gene and $4$ pairs with two genes), and $r=4$,
calculation of the sum above gives: $p_{457,80,4} \approx 0.743$.
May 27, 2015 at 11:02 am
J.J. Emerson
For the H0 of randomly distributing 80 “accelerated” genes amongst 457 gene pairs, oz’s answer generates the appropriate cdf. The counting argument makes sense to me and a quick and dirty simulation in R I did yields the same Monte Carlo cdf to within 0.17% for r = 4 (e.g. 0.74469 vs 0.74341). Plotting the cdf from 0 to 12 on the same chart yields visually indistinguishable results (ie 0.17% isn’t a difference you can see on a cdf plot).
Of course posing a different H0 changes everything, and there is enough history in the duplication evolution field to suggest virtually any H0 you care to imagine. Not that they are all equally reasonable to my mind, by whatever.
May 26, 2015 at 6:42 am
Lior Pachter
The following answer was submitted to me by email, by someone who wrote it up in April 2004. This someone sent the writeup to the authors at the time, but apparently no response was received. The someone approves this anonymous submission in response to my blog post (11 years later).
==========================================================
The evolutionary fate of duplicated yeast genes
(names redacted)
April 27 2004
The evolutionary fate of duplicated genes has long puzzled biologists [1]. This topic can now be addressed directly, thanks to the work of Kellis et al [2]. Kellis et al. sequenced the yeast species Kluyveromyces waltii, and showed that its ancestor diverged from the ancestor of Saccharomyces cerevisiae shortly before a whole-genome duplication event. Although most of the duplicated S. cerevisiae genes have since lost one copy by deletion, the surviving duplicated gene pairs are of great interest. Ohno hypothesized that in such cases one gene copy should evolve slowly, while the evolution of other, paralogous copy will accelerate [1]; others have argued against this model [3-5]. Kellis et al. interpret their data as support for the Ohno model [1]. As we show here, however, the frequency of accelerated evolution in one gene copy is independent of acceleration in its paralogous copy, in the test used by Kellis et al. In fact, duplicated S. cerevisiae genes evolve at significantly more similar evolutionary rates than expected at random, in contradiction to the Ohno model.
Of the 376 S. cerevisiae paralogous gene pairs identified by Kellis et al. (excluding the pairs that have undergone gene conversion [2]), 76 pairs exhibit accelerated protein evolution, defined as instance in which the amino acid substitution rate along one or both of the S. cerevisiae branches was at least 50% greater than the substitution rate along the K. waltii branch [2]. Kellis et al. note that “strikingly, in nearly every case (95%), accelerated evolution was confined to only one of the paralogues. This strongly supports the [Ohno] model in which one of the paralogues retained an ancestral function while the other, relieved of this selective constraint, was free to evolve more rapidly” [2].
Although 95% sounds like a striking proportion, it does not in fact imply that accelerated evolution preferentially occurs in only one gene copy. To the contrary, we would expect to find the observed pattern of acceleration even if the evolutionary rates of duplicated genes were completely independent of one another. Among the 752 genes under consideration, 80 genes exhibit accelerated evolution. Therefore, under the parsimonious null model of independent evolution, we would expect 376 × (80/752)2 = 4.26 pairs in which both copies exhibit acceleration, which is not significantly different from the four such pairs observed (P = 0.58, binomial test). Because the frequencies of acceleration in duplicated S. cerevisiae genes are consistent with a simple null model of independence, they do not support Ohno’s model of duplicate gene evolution.
Although it has been convenient to analyze the pattern of “accelerated evolution”, defined by a threshold rate of substitution [2], the full distribution of evolutionary rates is much more informative. The mean absolute value difference in evolutionary rates between the pairs of duplicated S. cerevisiae genes is 0.413 (rates expressed relative to K. waltii orthologs, as calculated by Kellis et al.). If we repeatedly permute the pairings between the 752 genes, the mean difference between randomized pairs is 0.506 ± 0.012 (± one SD). In other words, the paralogous S. cerevisiae genes are much more similar in their evolutionary rates than randomly paired genes from the same pool (P < 10-14). This result contradicts Ohno’s model, which predicts that paralogous copies should exhibit significantly different evolutionary rates.
Page 1/2As noted by Kellis et al., the slower evolving gene in a duplicated pair is essential for viability significantly more often than is the faster evolving copy. Furthermore, we find that the expression levels [6] of the slow copies are significantly greater than those of the fast copies (P < 10-6, Wilcoxon test). These observations alone do not support Ohno’s model, however, given that in the S. cerevisiae genome as a whole slower evolving genes are known to be significantly more essential [7] and expressed at significantly higher levels [8].
While there may be several cases of duplicated S. cerevisiae genes whose evolution follows Ohno’s classic model, we have shown here that the vast majority of duplicated genes evolve at significantly similar rates. The most simple explanation of this trend is that, in contrast to Ohno’s hypothesis, duplicated yeast genes tend to retain at least broadly similar functions, and thus exhibit similar levels of selective constraints over evolutionary time.
1. Ohno, S. Evolution by Gene Duplication (Springer-Verlag, New York, 1970).
2. Kellis, M., Birren, B.W., and E.S. Lander. Proof and evolutionary analysis of ancient
genome duplication in the yeast Saccharomyces cerevisiae. Nature 428: 617-624 (2004)
3. Clark, A. G. Invasion and maintenance of a gene duplication. Proc Natl Acad. Sci USA
91: 2950-2954. (1994)
4. Hughes, A. L. The evolution of functionally novel proteins after gene duplication. Proc.
R. Soc. Lond. B Biol. Sci. 256:119–124. (1994)
5. Lynch, M. and A. Force. The probability of duplicate gene preservation by
subfunctionalization. Genetics 154, 459–473 (2000).
6. Wang, Y., Liu, C. L., Storey, J. D., Tibshirani, R. J., Hershlag, D., and P. O. Brown.
Precision and functional specificity in mRNA decay. Proc. Natl. Acad. Sci. USA
99:5860-5865 (2002).
7. Krylov, D. M, Wolf, Y. I., Rogozin, I. B., Koonin, E. V. Gene loss, protein sequence
divergence, gene dispensability, expression. Genome Res 13:2229-2235 (2003)
8. Pal, C., Papp, B. and L. D. Hurst. Highly expressed genes in yeast evolve slowly.
Genetics 148:927-931 (2001)
May 26, 2015 at 7:14 am
bride of frizzled disco
If my memory serves me, this was submitted to Nature as a response to the KBL paper. I know this because I submitted a similar rebuttal at the time. Nature declined to publish these as they felt they did not detract from the central message of the paper.
May 26, 2015 at 8:56 am
Michele Busby
We also published something along the lines of this: “Furthermore, we find that the expression levels [6] of the slow copies are significantly greater than those of the fast copies (P < 10-6, Wilcoxon test)"
In cross species RNA Seq, the slower moving copy of a duplicated Bayanus gene had expression similar to the cerevisiae and the more diverged loss expression.
Here: http://www.biomedcentral.com/1471-2164/12/635
Figure 5
But our data is noisy and our Ns are low as there weren't many duplicates so I don't think our result is definitive (but it supports a model where one is maintained and the other loses function).
It might be worth repeating with more data and newer sequencing protocols. There are also other bigger datasets now. I don't know if anyone did something similar.
May 26, 2015 at 6:55 am
Andrew Drake-Brockman
It’s a long-shot:
Given that each outcome in the sample space Ω is equally likely, the probability of an event A is the following formula:
\mathrm{P}(A) = \frac{|A|}{|\Omega|}\,\ \left( \text{alternatively:}\ \Pr(A) = \frac{|A|}{|\Omega|}\right)
Assuming Ω is an infinite set, and A is the event in question, for which you want a p derived for, and assuming A is the event of the realization of the alternative hypothesis, then p=0.
My assumptions are questionable but the mathematics is valid. You now owe me $∞.
May 26, 2015 at 9:44 am
Harry Hab
I can answer your bonus question: Nature is a corrupt rag run by failed post-docs.
May 26, 2015 at 9:44 am
Ben
The analysis seems quite reasonable to me: https://github.com/BenjaminPeter/kellis/blob/master/kellis.pdf
May 26, 2015 at 10:23 am
Burner Account
Maybe we should treat the word “strikingly” as “interesting enough to the author to be worth pointing out” instead of artificially attaching the significance of a p-value to it.
Don’t get me wrong, Nature publications should be beyond reproach, but perhaps the real story here is that too often, we make the assumption that “strikingly” or “interestingly” are synonyms for “statistically significantly”.
May 26, 2015 at 10:27 am
Lior Pachter
The point of the p-value prize is precisely to see whether we can crowdsource an answer to “is it interesting enough to point out?”
May 27, 2015 at 6:06 am
Manolis Kellis
See my response below. When distinguishing between the Ohno model (asymmetric acceleration) and the alternative proposed of symmetric acceleration, we find astronomical p-values for 72 of 76 pairs being asymmetric. Yes, this focuses on the most extreme acceleration, but it’s hugely significant. My issue with the (names redacted) shuffling is that they ignore gene pairs, and thus assume that acceleration is independent of the specific biological gene function, which i doubt it really is. You owe me some cash 😉
May 26, 2015 at 12:08 pm
Michael Eisen
I’ve tried a bunch of different models, and so far the most charitable I can come up with is to look just at the number of singletons, ignoring the number of doubles/zeros you get. If you assume the p of a single hit is 80/914 = 0.087527352, then the probability of an unpaired hit is 0.15973263, and you end up with >= 72 with p ~ .5691, which looks pretty bad for the authors.
However, we’re forgetting about multiple testing. Since they only did one statistical test, while the typical genomics experiment at the time did > 20, you have to divide this p value by 20 to bring it into line with the rest of the field. So if you divide .5691 by 20 (which is conservative of course) you get p=0.028455, which means you conservatively owe me $3,514.
May 26, 2015 at 1:27 pm
John Smith
The number of tests done at the time is irrelevant, its the size of the hypothesis space that matters, which doesn’t depend on the number of tests performed or not. But more importantly, why are you dividing p by 20, you should divide the critical value by 20 for a Bonferroni correction. Equivalently you can multiply p by 20. You’ve won $8.79.
May 26, 2015 at 4:12 pm
Michael Eisen
Umm, because I’m trying to point out the absurdity necessary to get to a significant p-value???
May 27, 2015 at 9:17 am
darachm
A p-value of 11.3 ? Sounds legit …
June 9, 2015 at 11:45 am
caseybergman
When applying a Bonferroni correction for multiple tests one does not either divide nor multiply the p-value generated by the test statistic under the null hypothesis given the data. The Bonferroni correction divides the alpha level cutoff considered “significant” for the test (e.g. 0.05) by the number of tests performed. The (incorrect) shorthand procedure of multiplying p-values by the number of tests leads to nonsense p-values, as darachm points out.
May 26, 2015 at 12:56 pm
biomickwatson
Out of 457 duplicated gene pairs, 76 are showing accelerated evolution in at least one gene.
They’re duplicated, being kept and evolving, so it would be wise to assume they are under positive selection.
Under that assumption, it follows that the original gene function must be important, so cannot be lost.
The expected frequencies are therefore 76 pairs where only one gene is rapidly evolving, and 0 pairs where both are (because if both were rapidly evolving, the original function would be lost). This is your null model.
The observed are 72 and 4, and Fisher’s exact test gives me a p-value of 0.12 (almost significant!)
You therefore owe me $83.3 (recurring, which means you will forever be in my debt)
June 5, 2015 at 7:41 am
K
Here’s my best attempt to win all of Lior’s money using the McNemar (exact) test. The specific model of evolution tested is that WGD increases the chance for a gene to be accelerated.
There are 381 pairs with 0 genes accelerated. We can infer the parent gene was not accelerated pre-WGD and the duplicate genes were also not accelerated post-WGD.
There are 72 pairs with exactly 1 gene accelerated. We can infer that the parent gene was not accelerated pre-WGD and 1 of the duplicates underwent accelerated evolution post-WGD.
There are 4 pairs with 2 genes accelerated. These were either 1) accelerated pre-WGD and also accelerated post-WGD or 2) accelerated pre-WGD but not accelerated post-WGD or 3) not accelerated pre-WGD but accelerated post-WGD. But 4 is a small number and won’t matter in the hypothesis test I’m proposing.
Putting these numbers into a 2×2 table, we can run a McNemar exact test to see if the WGD had any effect on the chance for the gene to be accelerated. For the purposes of this post, I’ll interpret this to be the specific model of evolution mentioned in the abstract. Here’s the R output for one choice of distributing the 4 pairs with 2 genes accelerated. The p-value is x mcnemar.exact(x)
Exact McNemar test (with central confidence intervals)
data: x
b = 4, c = 72, p-value < 2.2e-16
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.01473863 0.14851329
sample estimates:
odds ratio
0.05555556
June 5, 2015 at 7:46 am
K
Sorry, the part that was cutoff was:
x <- matrix(c(381, 72, 4, 0), 2, 2)
June 5, 2015 at 10:52 am
K
Lior asked me to clarify my analysis a bit…
The odds ratio is ~0.06 which is in the 95% confidence interval and is far from 1 (see the alternative hypothesis). The P-value for this example is for the case where all 4 genes with 2 accelerated copies are assigned as accelerated pre-WGD but non-accelerated post-WGD (hence b = 4). There are other assignments possible as I described above but all result in a similar P-value.
And finally to clarify the inference of acceleration pre- and post-WGD, for a first pass one can think of non-acceleration as being 0 substitutions and acceleration as being 1 or more substitutions.
June 6, 2015 at 8:53 am
astoltzfus
K, I’m baffled by this. Can you explain? You seem to be creating a contingency table where the columns are “no” and “yes” for “accelerated pre-WGD”, and the rows are “no” and “yes” for “at least one member accelerated post-WGD”.
x <- matrix(c(381, 72, 4, 0), 2, 2)
x
[,1] [,2]
[1,] 381 4
[2,] 72 0
Then the first column (for pairs not accelerated pre-WGD) has row-values (1) 381 pairs not accelerated post-WGD, and (2) 72 pairs accelerated post-WGD. The second column has (1) 4 pairs not accelerated post-WGD, and (2) 0 pairs accelerated post-WGD.
Is that right?
Next question. I get the same "p-value < 2.2e-16" with mcnemar.exact(x), but I don't see how anything that works like a contingency test can possibly give significance for the above distribution of numbers. For instance, chisq.test(x) gives p = 0.86. What is the mcnemar test doing that makes this result seem striking?
Next question. You state that the 4 pairs with both members accelerated might go into any of 3 cells (all but upper left), but you put them all in one cell on the grounds that it is a small number and doesn't matter.
Actually, that seems to be correct for the mcnemar test. For instance, if I change column 2 from (4, 0) to (1, 3) I get exactly the same P value:
x2 mcnemar.exact(x2)
Exact McNemar test (with central confidence intervals)
data: x2
b = 1, c = 72, p-value < 2.2e-16
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.0003468794 0.0798859954
sample estimates:
odds ratio
0.01388889
Or if I swap the rows in the first column, I also get the same p value:
x3 mcnemar.exact(x3)
Exact McNemar test (with central confidence intervals)
data: x3
b = 1, c = 381, p-value < 2.2e-16
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
6.627918e-05 1.471177e-02
sample estimates:
odds ratio
0.002624672
June 6, 2015 at 8:56 am
astoltzfus
The alternative matrices got substituted in my message.
x2: matrix(c(381, 72, 1, 3), 2, 2)
x3: matrix(c(72, 381, 1, 3), 2, 2)
June 6, 2015 at 9:37 am
K
astoltzfus: Yes, your analysis is all the same as mine. A regular Fisher’s exact test would not give a significant P-value which is why I am using McNemar’s exact test instead. It’s basically the paired version of Fisher’s exact test where the pairing is between the parent gene and the two duplicates post WGD.
To see the striking thing about the contingency table, consider the row and column sums. In my original example, there were 453 genes not accelerated pre-WGD and 4 genes accelerated pre-WGD (these are the column sums). Importantly, no matter how you assign the 4 genes, there are *at most* 4 genes accelerated pre-WGD.
However, post-WGD, things change a lot: 385 genes are not accelerated but now 72 genes are accelerated (these are the row sums).
What do you think?
June 6, 2015 at 9:48 am
K
Woops, I shouldn’t have admitted I tried 2 hypothesis tests… will Lior now cut my prize money in half to account for multiple testing?
June 6, 2015 at 11:28 am
ot
I think K’s analysis sounds about right. He/she is testing the hypothesis of whether the P(pre-WGD acceleration) is the same as the P(post-WGD acceleration). By doing so, he/she is testing the effect of WGD on the acceleration of duplicate pairs, as he/she has said, which seems to me to be a relevant question to the context.
But to be more convinced, I would love to see the statistics/contingency tables for other thresholds of defining acceleration (currently it is >50%) to confirm the robustness of the claim.
June 6, 2015 at 5:51 pm
ot
Erik’s analysis made me realize that one cannot rule out the possibility of simple independent evolution that seems to be consistently fitting the data with various threshold selections, while the 95% claim becomes less impressive at other thresholds. Perhaps a justification for the threshold selection is needed from the author. But I do feel that even with this oversight the paper still deserves merit for “proving the evolutionary history of WGD” as the title of the paper suggests because the 95% claim is a relatively minor one as Pavel says. By the way, the entire abstract is in boldface!! So it is rather unfair to pick one sentence from it to criticize when you don’t discuss the other contributions of the paper. We are giving Kellis such a hard time. Perhaps the lesson to be taken away from graduate students like myself is to be always skeptical of one’s finding, and discuss work with many other people to discover potential oversight.
June 7, 2015 at 12:56 am
Erik van Nimwegen
Dear ot,
I totally agree that the result we are currently discussing is not at all the main result of the paper, which was the extensive evidence for WGD in S. cerevisiae. The paper is rightly considered important for this!
So it is indeed unfortunate if students now get the impression that somehow the key results of the paper are being called into question. They are not.
From the start I thought Lior was just drawing our attention, in his usual compelling way, to a rather blatant statistical ‘error’ in a well-known paper. I personally just assumed that KBL made an honest mistake and simply didn’t realize that the 95% is what you expect under a simple model of independent evolution.
What is surprising to me and some others, is that the authors seem to stand by their original interpretation. I think Mike Eisen did a good job of explaining why this is disappointing to some of us.
May 26, 2015 at 1:38 pm
dmitristanford1234
On the simplest model of uncorrelated and independent rates of evolution of the duplicates, you expect to see ~6 pairs (457*(76/914)^2) and it is clear that the data would not reject it. The null could be that the two paralogs have the same rate of evolution and the data might then reject it easily as most paralogs do seem to have very different rates of evolution as far as I remember. You might want to define your challenge a bit narrower:)
May 27, 2015 at 6:08 am
Manolis Kellis
Yep, your alternate null (symmetric vs. asymmetric acceleration) is what we stated in the paper. Hugely significant
May 26, 2015 at 2:36 pm
nsaunders
I haven’t though about the p-values, but I did once think about the use of sentence adverbs such as “strikingly” in scientific articles.
May 26, 2015 at 7:43 pm
Michael Eisen
The more I think about this, the more I think that I and many others here are approaching this the wrong way. Kellis’s claim is that the rates of evolution of gene pairs are uncorrelated. As many of us have shown, the data they present is more or less spot on what you would expect if gene evolve independently – the high p-values when trying to reject independence being exactly what they would predict given their claims of independence. Of course, as the post from (names redacted) points out the real way to evaluate their claim is to look at the actual rates, and that the use of an arbitrary cutoff (without real justification) is bogus. But that aside, it seems to me that the real problem here is not a statistical one, but rather a failure to be even marginally skeptical about ones assumptions and results – something calls for better p-values won’t fix.
May 27, 2015 at 5:14 am
Joshua Plotkin
I’m interested in why you say that, Michael, or whether you meant to say “anticorrelated” instead of “uncorrelated”?
Kellis et al claim their data support Ohno’s theory — that one copy of a retained duplicate pair should retain the ancestral function and the other copy should diverge in function, so that their evolutionary rates are predicted to be anti-correlated.
“(names redacted)” seem to interpret the central claim of Kellis et al correctly, and they explain that the data don’t support this claim. The distribution of evolutionary rates (as opposed to using arbitrary thresholds) actually seem to support the opposite view: duplicate copies tend to have correlated evolutionary rates.
Most of the p-values proposed in the comments (the desire to avoid duplicate posts notwithstanding) are based on a null hypothesis of independent rates, which seems to me the obvious, and correct, null for testing the claims of KBL. No?
May 27, 2015 at 7:28 am
Michael Eisen
Right. Ohno predicts that they should not just be independent but anti-correlated, so using a null model of independence makes sense.
June 5, 2015 at 2:31 pm
Manolis Kellis
Dear Mike and Joshua, thanks for weighing in. It seems that your interpretation of Ohno 1970 is that the *only* mechanism for duplicate preservation is neofunctionalization. This was certainly the claim in Force 1999, but is directly contradicted by Ohno’s own writing. As i wrote in my comment to Pavel and his class here https://liorpachter.wordpress.com/2015/05/26/pachters-p-value-prize/#comment-4436 Ohno 1970 proposed multiple mechanisms for maintaining duplicated genes – including gene dosage and gene conversion (chapter X), heterozygous advantage by fixation of two alleles (chapter XI), differential regulation (chapter XII), and new gene functions (chapter XIII) which ‘might finally’ arise. Thus, Ohno’s model (at least as Ohno described it) does not predict anti-correlated evolution for all preserved gene pairs, but merely that those pairs that show acceleration will tend to do so asymmetrically.
May 27, 2015 at 5:58 am
Manolis Kellis
Our paper was quite explicit about the null model being tested. We wrote: “Two alternatives have been proposed for post-duplication divergence of duplicated gene pairs. Ohno has hypothesized that after duplication, one copy would preserve the original function and the other copy would be free to diverge[1]. However, this model has been contested by others, who argued that both copies would diverge more rapidly and acquire new functions [20–22].” In other words, we sought to distinguish between the Ohno one-gene-only speeds-up (OS) model and the alternative both-genes speed-up (BS) model. We did not allow a null model to independently shuffle genes between pairs (IS) as it would imply that the probability of acceleration does not depend on the specific biological function of the genes in question, which is my issue with the blind shuffling of genes between pairs in the (names redacted) comment from April 2004.
Given this explicit goal and assumption, we focused on 76 accelerated gene pairs, and found that 72 of 76 accelerated pairs are asymmetric (95%), which leads to rejection of the BS null model that accelerated evolution works on both genes rather than only one. To provide the missing P-value using binomial statistics, we can draw pairs of asymmetric balls with probability p_as under the OS model, and draw pairs of symmetric balls with probability p_s under the BS model. Making the assumption that the OS and BS models are each claiming to be right 95% of the time (p_s=p_as=0.95), we have 72 successes in 76 trials and success probability p_a=0.95 in the OS model, leading to P_OS=0.2, and we have 4 successes in 76 trials with a success probability p_s=0.95 under the BS model, leading to P_BS=2.2*10^-88. In a likelihood ratio framework, the Ohno model is 10^87 times more likely, leading to significant rejection of the BS null, and a cash prize of 903,659,165 million billion trillion quadrillion quintillion sextillion dollars, which LP can choose to award in 2015, 2004, 1970s, or 1930s dollars. (Even with p_s=p_as=55%, which is quite low confidence for most scientists, LP still owes me $84 million)
May 27, 2015 at 6:20 am
Dr. No.
This is what is wrong with p-values in general. One can actually make up any number whatsoever – then we’ve left arguing about the null model setup rather than focusing on the statement itself.
One does not even need to read or understand what MK wrote up above to know that it is incorrect – it is obviously wrong because it has a p value pf 10^-88 that alone proves it.
There is no realistic biological phenomena in the world that would be known to that level of certainty. Hence the null model that is used must be wrong.
May 27, 2015 at 6:29 am
Pseudo
It seems unfortunate to name a reasonable null hypothesis “the BS null model”
May 27, 2015 at 7:01 am
Dr. No.
LOL,
the name “the BS null model” is actually perfect – that is exactly what is going on,
thanks for pointing it out Pseudo.
May 27, 2015 at 7:38 am
Joshua Plotkin
Interesting; and thanks for the forum, Lior.
The model called “both-genes speed-up (BS)” is more commonly known as the duplication/degeneration/complementation (DDC) model.
Both the Ohno model and the DDC model make specific, positive claims about the behavior of preserved duplicate genes, as compared to genes that are just singletons. And so a reasonable test of either model should compare the properties of preserved duplicates to the properties of all genes. (Neither the Ohno model nor the DDC mode can be used as a NULL, since they both make positive claims.)
In particular, Ohno posits that one copy will retain a single ancestral function and the other copy will evolve a new function (and so presumably one evolves at a slow rate, and the other more quickly); DDC posits that the ancestral gene performed multiple functions which are then partitioned between the duplicate copies, each of which experiences relaxed selective constraint.
An ideal way to distinguish between these two models is by direct complemetation experiments — which is what van Hoof (PMID 15965245) did. He concluded that all four cases tested rejected the Ohno model in favor of the DDC model. van Hoof specifically tested the ORC1/SIR3 pair, which was highlighted by KBL as a posterchild of Ohno’s model, and found no derived/novel function of SIR3 whatsoever!
An analysis based on evolutionary rates alone is less definitive, because it cannot reliably ascribe new or non-complementary functions. In any case, such an analysis must presumably first ask whether the data support either the Ohno or the DDC models at all, over the obvious null that retained duplicates are no different than random pairs of genes.
“My issue with the (names redacted) shuffling is that they ignore gene pairs, and thus assume that acceleration is independent of the specific biological gene function, which i doubt it really is”
Ignoring the pairing of duplicates as the null hypothesis is precisely what we *should* do when we suspect, and wish to show, that duplicated genes have unusual patterns of evolutionary rates compared to singletons. This is presumably why most readers of the blog immediately thought to compare to a null model of independence.
I guess the larger point is the problem of conditioning the analysis on at least one accelerated gene copy, according to an arbitrary threshold. If we want to study the Ohno or DDC models how can we possibly ignore the 381 (of 457) pairs that don’t show any “acceleration” at all?
May 27, 2015 at 8:07 am
Manolis Kellis
Our hypothesis as stated in our paper was that “along with *possibly* gaining a new function, the derived copy has lost some essential aspect of its function, and cannot typically complement deletion of the ancestral gene”. The van Hoof experiments are great, but do not resolve whether Sir3 “lost some essential aspect” of the ancestral Orc1/Sir3 dual function, as proposed in our paper. Has anyone carried out the converse experiment from van Hoof, of whether S. cerevisiae Sir3 or Orc1 alone/jointly complement deletion of the non-duplicated Orc1/Sir3 gene in the non-duplicated species? Our paper’s prediction would be that Orc1 may still complement, but that Sir3 would not complement. The fact that the non-duplicated gene complements Sir3 does not immediately imply the converse
May 27, 2015 at 8:49 am
Joshua Plotkin
KBL infers definitively that Sir3 evolved a new function, based on its accelerated rate of evolution; whereas van Hoof rejects this contention by experiment.
But little can be gleaned from a single example. The bigger issue remains: to test either the Ohno or DDC models using evolutionary rates alone, the only reasonable null hypothesis is that duplicate genes are no different from random pairs of genes.
May 27, 2015 at 2:51 pm
Devin Scannell
Joshua, I disagree that the bigger issue is the null hypothesis for distinguishing the Ohno or DDC models based on sequence. The fact that the van Hoof experiments directly contradict the sequence analysis that naively appeared to support the Ohno model should remind us that *evolutionary rates are not functional assays*. Every one of us can point to an example where a single substitution either eliminated or radically altered function. The idea that we can construct a simple linkage between rates and function has somehow propagated through the literature but it is basically just an awkward assumption. Per my previous comment, this question requires functional data.
There are two bodies of work that are relevant. The models for duplicate preservation make sense when you cast things in terms of gain-of-function and loss-of-function but it is notable that Lynch and colleagues never talk about sequence. Because they can’t. On the other side, Joe Thornton has gone furthest in exploring sequence (-> structure) -> function relationships for duplicates and without this level of rigor there will always be alternative models that explain the data. Much more intelligent models/analyses can help but unless they are supported by experiments people will simply not be convinced.
Final point, if all we wanted was a a very general statement about whether DDC or neofuncitonalization is more common on average, the simulations done by Force, Lynch and others show that this reduces to knowing the effective population size. For a more nuance one could think through real-world violations of Hardy Weinberg assumptions and the particulars of (yeast) genome structure and mating habits. The likely short answer is that after a WGD, population size is small so neofunctionalizing mutations will be rare. The van Hoof experiments provide the empirical support this*. A few more complementation experiments would probably close the chapter and put the neofunctionalization model to the sword (at least as far as yeast WGD goes)**.
Any wet-lab folks want to collaborate on this? 😉
* PM me for the caveats on why this may not be true in detail, only as a first order assessment
** It is probably much more complicated than this — initial duplicate preservation and long term duplicate evolution can look very different. Discussed a little in my Genome Res paper….
May 27, 2015 at 9:36 am
Manolis Kellis
I simply don’t buy the fully random-pairs shuffling of genes as a control for ohnologs, as it confounds common functional class and common evolutionary history. Genes with common function are more likely to show similar acceleration/deceleration in response to changing environments. For Sir3(YLR442C), acceleration by itself is consistent with either neofunctionalization or specialization, but the deletion experiments cited in our paper [29-30] indicate that Orc1 likely complements loss of Sir3 (non-lethal) while Sir3 doesn’t complement loss of Orc1 (lethal) (S9 http://www.nature.com/nature/journal/v428/n6983/extref/S9_Trees/Duplicated_Pairs.xls ). For the curious, the protein alignment may offer some clues as to how much we could have predicted from sequence alone (S8 http://www.nature.com/nature/journal/v428/n6983/extref/S8_DupGenes/YLR442C_YML065Wp.txt ). I think the message is clear that there’s only so much that an initial computational study can do, and 11 years later, many experiments remain to be conducted (including the reverse complementation, and forward/reverse complementation for many more pairs). In 2004, this was still the first comparison (with Ashbya http://www.ncbi.nlm.nih.gov/pubmed/15001715) across a whole-genome duplication. Since then, there’s been a lot of new understanding by you and many others. Let’s not ignore the value of genomic studies prior to systematic experimental probing.
May 27, 2015 at 1:58 pm
p.value
p-values depend only on the distribution of the data under the null hypothesis. I don’t think what Manolis described above is a p-value as it depends on the alternative hypothesis as well. People here have focused on the choice of null hypothesis or the flaws of p-values in general (I agree with the general sentiment on both issues), but I think we need to step back and understand what a p-value is. It has a rigorous definition, once the data and the null model are specified.
June 4, 2015 at 9:08 am
Johannes Soeding
This answer from such a preeminent researcher as Manolis Kellis is curious and troubling. It is the highlight of a discussion that starkly illustrates the importance for scientists of being able to admit ones one mistakes.
1. Manolis computes two p-values, one for a “BS hypothesis” and one for a “OS hypothesis” Let’s call n = 80 the number of duplicated gene pairs for which at least one gene shows accelerated evolution, and let k = 4 be the number of gene pairs among these for which both genes show accelerated evolution.
What Manolis computes is this:
P-value(BS_Kellis) = (n choose k) (1-k/n)^k (k/n)^(n-k)
= (80 choose 4) 0.95^4 * 0.05^72 = dbinom(4,76,0.95) = 0.1996
P-value(OS_Kellis) = (n choose k) (1-k/n)^(n-k) (k/n)^k
= (80 choose 4) 0.95^72 * 0.05^4 = dbinom(72,76,0.95) = 2.219E-88.
Apart from the fact that Manolis forgot to sum over the more extreme events,
P-value(BS_Kellis_corrected)
= sum_{l=0}^k (n choose l) (1-k/n)^l (k/n)^(n-l)
P-value(OS_Kellis_corrected)
= sum_{l=0}^k (n choose l) (1-k/n)^(n-l) (k/n)^l
= 1 – P-value(BS_Kellis_corrected),
the null model “BS_Kellis” which he rejects with his calculation and which he equates with the BS hypothesis is: “The probability for a pair of genes to both have accelerated rates is 0.95”. This hypothesis is of course pure nonsense and has nothing to do with the real BS hypothesis. (Note that this straw man “BS hyppothesis” depends on Kellis’ arbitrary choice of cut-off for selecting accelerated genes.) Likewise, his alternative null model, which he equates with the OS hypothesis, is: “The probability for a pair of genes to NOT both have accelerated rates is 0.95”, which is equally absurd.
What is his logic for the choice of 0.95? He writes “.. the OS and BS models are each claiming to be right 95% of the time (p_s=p_as=0.95)”. This statement is hard to make sense of since in hypothesis testing we assume that the null hypothesis is correct for *all* the data, of course, not just for a part of it. It must have been very late when he wrote his blog post.
2. In his a blog post from May 27, 9:37 AM, Manolis writes: “I simply don’t buy the fully random-pairs shuffling of genes as a control for ohnologs, as it confounds common functional class and common evolutionary history. Genes with common function are more likely to show similar acceleration/deceleration in response to changing environments.” Here, he seems to have forgotten that he corrects for the dependence of mutation rates of genes on their function and evotionary history by comparing the mutation rates in the duplicated gene pair with the rate of the orthologous gene in the K. waltii branch.
3. As an illustration of the situation, here is a simulated distribution of mutation rates rate_1 and rate_2 in pairs of duplicated genes, normalized by the rate in K. waltii, rate_ref, in a log-log plot. The lines correspond to the acceptance threshold of 1.5 for accelerated evolution used by Kellis et al. in their 2004 paper. I simulated the 457 pairs as isotropic 2-dimensional Gaussian distributions with sigma = sqrt(0.1). In the run shown, 80 gene pairs fall to the right or upper side of the thresholds and 4 show accelerated evolution in both genes. Note that according to the Ohno hypothesis we would expect a negative correlation, since we expect one of the genes to evolve faster than the other. It is obvious from this illustration that, based on the numbers k and n found in the Kellis paper, the BS hypothesis explains the data rather better than the OS hypothesis, and certainly the BS hypothesis cannot be rejected.
June 5, 2015 at 2:39 pm
Manolis Kellis
Dear Johaness, thanks for your comments and thoughts. Some quick replies to your points.
1. Yes, you’re right, I calculated P-values for the exact count, but the integral/sum would have been slightly better, and the likelihood ratio even more significant. Yes, you’re right, that parameter is quite arbitrary, but the likelihood ratio remains significant for almost any values between .5 and 1. My post reported the ones at .95 and .55. At 1, the likelihood ratio simply explodes (and the prize money becomes infinite).
2. The division corrects for rate, but not for acceleration. My comment, which you pasted correctly, was that the acceleration/deceleration in response to changing environments will also depend on the gene function, not just the base rate. Note that the random-shuffling model also predicts that gene loss in duplicated regions will be random, which is inconsistent with the data (see comment #2 in my comment to Pavel here https://liorpachter.wordpress.com/2015/05/26/pachters-p-value-prize/#comment-4436 )
3. Unfortunately, your graph did not come through. However, Ohno 1970 simply does not predict that acceleration will be negatively correlated for all gene pairs, simply for those gene pairs that show acceleration. He proposes many mechanisms for post-duplicate gene preservation, only one of which is gain of new functions (see comment #1 in the same comment to Pavel and his class https://liorpachter.wordpress.com/2015/05/26/pachters-p-value-prize/#comment-4436 )
May 26, 2015 at 8:22 pm
Pseudo
The most reasonable null model that I can justify is
H0: the rates of evolution (classified as accelerated or not) of individual genes in a duplicated pair are independent.
Based on the language “Strikingly, in nearly every case (95%), accelerated evolution was confined to only one of the two paralogues,” I’ll consider the likelihood of observing 4 or fewer pairs harboring both genes under accelerated evolution, given H0. This is slightly disingenuous (on my part), since the language seems to imply that the intended null is something more along the lines of “both copies diverge rapidly and acquire new functions (i.e., exhibit accelerated evolution, see p. 621 in original paper).” But I don’t believe I can support this null, so I’m starting with the model that paralogs evolve independently.
As discussed in the above comment (GM), the probability that a single gene exhibits accelerated evolution is estimated by p=80/914. The 457 pairs therefore represent binomial experiments, for each of which the number of paralogs, X, under accelerated evolution is
X~Bin(2,p)
So the probability of observing both paralogs under accelerated evolution, assuming independence, is
P(both genes under accelerated evolution | H0)=choose(2,2)*(p^2)*(1-p)^0=p^2
If we let q=p^2, then the number of pairs, Y, out of 457 in which both paralogs exhibit accelerated evolution is
Y~Bin(457,q)
The likelihood of observing 4 or fewer such pairs is then
P(Y<=4)=P(Y=0) + P(Y=1) + P(Y=2) + P(Y=3) + P(Y=4)
P(Y=0)=choose(457,0)*(q^0)*(1-q)^457
P(Y=1)=choose(457,1)*(q^1)*(1-q)^456
P(Y=2)=choose(457,2)*(q^2)*(1-q)^455
P(Y=3)=choose(457,3)*(q^3)*(1-q)^454
P(Y=4)=choose(457,4)*(q^4)*(1-q)^453
P(Y<=4)=0.7256024
In agreement with the previous post.
However, I think the specific question of “how likely is 95%” depends on both the number of pairs in which both paralogs are under accelerated evolution as well as the number of pairs in which a single paralog is under accelerated evolution (in order to calculate the relevant proportion).
Not wanting to get too far into the weeds on the ratios of binomials, I used R to run a few thousand samples of these 457 binomial experiments with X~Bin(2,p).
mean(sapply(1:10000, FUN=function(c) {x = 72/76)
I plotted a few examples with
hist(sapply(1:10000, FUN=function(c) {x <- table(rbinom(457,2,80/914))[2:3]; x[1]/sum(x,na.rm=T)}), xlab="", main="")
This suggests that 95% or more of accelerated pairs harbor exactly one accelerated gene ~64% of the time (p=0.64). Of note, the 10th percentile was somewhere around 92%–i.e., most pairs harboring either gene under accelerated evolution harbor exactly 1 gene under accelerated evolution, given H0 and the data reported.
June 9, 2015 at 4:31 am
Pseudo
I hadn’t bothered to correct the error in the way the first R command pasted/rendered, but I suppose now is a good time to clarify. It’s the same core function as the hist() call except with mean(…>=72/76):
mean(sapply(1:10000, FUN=function(c) {x =72/76)
May 26, 2015 at 9:18 pm
Jacob Corn
I think you’re asking about the wrong “p”. For some coffee-table journals/editors, P(acceptance|famous senior author) = 0.999.
Snarkiness aside, here’s an extremely naive question relating to the Pritchard RNA-seq analysis: I can intuitively see why neofunctionalization might lead to differential expression, but why does subfunctionalization imply differential expression? Couldn’t it be that the subfunctionalized children need to maintain the same expression as the bifunctional parent (and hence as each other) to maintain fitness?
May 26, 2015 at 9:35 pm
Devin Scannell
The sentence you highlight makes four claims. Three are false, one is meaningless.
(1) Strikingly, (2) 95% of cases of accelerated evolution involve only one member of a gene pair, (3) providing strong support for a specific model of evolution, (4) and allowing us to distinguish ancestral and derived functions.”
If you are in a hurry, jump to #4.
1. Surprisingly – Meaningless
I’ll come back to this at the end
2. 95% of cases of accelerated evolution involve only one member of a gene pair – False
This is an artifact of looking at very long branches and arbitrary cutoffs for “accelerated”. We measured rates of protein evolution on multiple branches after the WGD and showed that – on average – *both* members of a pair evolve faster than controls. Much faster on early branches.
Click to access 137.pdf
3. providing strong support for a specific model of evolution – False
Most – if not all – reasonable models of duplicate evolution are compatible with accelerated and asymmetric protein sequence evolution. Take a (deliberately) simple example of subfunctionalization by asymmetric degeneration of alternative protein domains. Imagine, an ancestrally two-domain and bifunctional protein where domain A is 50AA and domain B is 100AA. If subfunctionalization allows all AAs in the one domain to be substituted (no indel model!), then the rate in one duplicate will be 2X that in the other. For every more realistic model there is a perfectly acceptable null (neutral) model that also predicts accelerated asymmetric evolution.
To be clear: Models of duplicate preservation (most not actually being models of long term evolution; See Katju et al.) are useful tools but are not grounded in sequence analyses or designed to make predictions about rates of protein evolution. Accelerated asymmetric evolution could as easily be the null as the alternative hypothesis.
4. allowing us to distinguish ancestral and derived functions – False
This is embarrassing for the both the authors and Nature. Ambro van Hoof actually tested the Kellis results with an *experiment* (something that you should never do prior to submission!). He picked 4 asymmetrically evolving pairs from the Kellis dataset and tried to complement the deletions with a single-copy ancestral gene. In all 4 cases, the single-copy ancestral gene complemented KOs of BOTH S. cerevisiae duplicates. To say another way, neither duplicate (“fast” nor “slow”) showed any evidence of a “derived” function that was not present in the ancestor from before the whole-genome duplication. The authors could not have distinguished ancestral and derived functions because there were no derived functions.
http://www.ncbi.nlm.nih.gov/pubmed/15965245
1. Surprisingly – Meaningless
Well, it’s surprising that it got published.
A final thought. There are many good things about this paper but the central claims you highlight have been known to be incorrect since it was published. The van Hoof paper (and to a lesser extent my paper and others) have highlighted the mistakes and corrected the literature. I would have said that most people in the evolution field had assumed this paper had been off the scientific menu for almost a decade now. What needs to change in scientific communication so that the “self correcting” properties of the literature can operate a little more effectively?
May 27, 2015 at 5:42 am
Manolis Kellis
Some quick clarifications: (1) Yes, the use of the word strikingly is weird, could have skipped altogether, although the finding is indeed significant (see my next post). (2) our paper reported a prevalence of asymmetric evolution, which was the only thing that could be accomplished at the time, given the lack of an outgroup genome. Ken’s lab, and your work in particular, went a lot further since then, and acceleration for both copies makes sense, but does not invalidate asymmetry for the extreme cases. (3) Accelerated asymmetric evolution is exactly what we claimed. What we rejected was the null hypothesis of symmetric acceleration. (4) The complementation experiments are very elegant, and completely consistent with our paper’s claims, namely that the slower/”ancestral” gene can complement the faster/”derived” gene. The beauty of working with yeast is that deletion experiment results were already available, and we used them to show that in 18% of cases the ancestral version could complement the derived one, but in no cases did the derived version complement the ancestral one. We wrote “The derived paralogue is thus not essential under these conditions, either because it does not function in rich medium or because the ancestral paralogue can complement its function. Moreover, we infer that along with possibly gaining a new function, the derived copy has lost some essential aspect of its function, and cannot typically complement deletion of the ancestral gene.” This is completely consistent with the subsequent experiments.
June 4, 2015 at 2:58 pm
astoltzfus
Lan and Pritchard apparently have forgotten that Stoltzfus, 1999 (http://www.ncbi.nlm.nih.gov/pubmed/10441669) proposed a model for sub-functionalization of “gene activity” that includes quantitative sub-functionalization, what they refer to as partitioning the “dosage”. The model is formally analogous to the DDC model of Force, Lynch et al that appeared the same year. I say “have forgotten” rather than “were unaware” because I have pointed this out to Pritchard before. Do I have to change my name to “Mike Lynch” to get recognition?
I pointed out in 1999 that isozyme data from the 1960s and 1970s shows the same pattern that Lan and Pritchard are pointing to, in which one isozyme is consistently lower in activity (gene activity, i.e., expression * specific_activity) than the other, across a range of tissues.
As one of the progenitors of the DDC model, I do not agree with Josh or Kellis that the implication of the model is an equal speed-up in both copies.
Prior to the first change in a fresh pair of duplicates, each copy is equally expendable and has the same expected rate of evolution. So, they start out the same. The initially expected asymmetry in rates is 0.
However, after one copy gets the first hit, the expected rate of evolution in the *other copy* drops. This is true both for the quantitative and the qualitative sub-functionalization, but it might be easier to work out an exact model for the case of quantitative sub-functionalization. For instance, if one copy gets knocked down to 65 % activity (via reduced expression or reduced specific-activity), the rate of evolution in the other copy is reduced because it must maintain at least 35 % activity in order for the pair to suffice.
Where the expectation goes from there depends on the exact dynamics, because there is a bifurcation that leads on the one hand to loss of a copy, and on the other hand to persistence.
Thus, the expected asymmetry over time is exactly the kind of complicated mathy problem that Josh likes to tackle.
May 27, 2015 at 7:25 am
Lior Pachter
This solution was submitted to me by email. I am including it here for the record:
Let’s consider then 457 random variables (each gene pair), each taking on one of three states: no accelerated genes (0), one accelerated gene (1), and two accelerated genes (2). The null hypothesis is that both genes in the gene pairs are independently accelerated (or not). This reduces, then, to a test for independent assortment. We can use a Chi-square test (and others). In R:
> N = 457
> X = 76
> k = 72
> library(HardyWeinberg)
> x = c(N-X, k, X-k)
> HWAlltests(x, verbose=TRUE, include.permutation.test=TRUE)
Statistic p-value
Chi-square test: 0.085387402 0.7701251
Chi-square test with continuity correction: 0.003395195 0.9535349
Likelihood-ratio test: 0.082294532 0.7742117
Exact test with selome p-value: NA 0.7667116
Exact test with dost p-value: NA 0.9266479
Exact test with mid p-value: NA 0.6633468
Permutation test: 0.085387402 1.0000000
Thoughts? Unfortunately none are even remotely significant. Funding is tight.
May 27, 2015 at 11:28 am
psuedo ls
Same idea, but laid out a bit simpler in base R:
# Probability any gene is “accelerated”
P <- 80/914
obs <- c(4,72,381)
exp <- sum(obs) * c(P^2, choose(2,1)*P*(1-P), (1-P)^2 )
# Chi-square, violates the less than 5 rule, but still …
chistat <- sum( (obs-exp)^2 / exp )
p <- 1 – pchisq( chistat, df=2)
May 27, 2015 at 1:59 pm
psuedo ls
We rolled 3600 pairs of six-sided dice, and strikingly, 83.33% of cases of dice having a `5′ involved only one member of a dice pair, providing strong support for a specific model of dice rolling.
May 27, 2015 at 8:29 pm
Joshua Plotkin
Pseudo ls 1:59pm clearly deserves the prize.
May 28, 2015 at 11:35 am
psuedo is ver2
The following corrects the computation errors in the psuedo Is at May 27, 2015 at 1:59 pm. This version is more complete and 91% is closer to 95% in the original paper.
Of the 3600 pairs of rolled six-sided dices, 1100 pairs had at least one ‘5’. Of the 1100 pairs, only 100 pairs had both ‘5’s.
Strikingly, 91% (1000/1100) of pairs of dices with at least one ‘5′ involved only one member of a dice pair, providing a strong support for a specific model of dice rolling,…
May 30, 2015 at 7:06 am
psuedo ls
Oi, yep, ignored the 2 ways.
May 27, 2015 at 5:56 pm
More than 3rd reviewer
I had to chime in, as this is possibly the most interesting discussion of models of gene duplication I have seen in a while. I don’t really care about the p-value question, as asymmetric evolution is not a unique prediction of the neofunctionalization model (see He and Zhang 2005, Genetics). I also don’t really care that the specific DDC model is being confused with the larger model of subfunctionalization, or Ohno is only getting credit for the neofunctionalization model even though he clearly articulated subfunc, too.
What finally made me have to write was Devin’s claim that the Force and Lynch model and simulations tells us anything about the relative frequencies of sub- and neofunctionalization. No, they don’t. All they say is that subfunctionalization via DDC will be more common in smaller populations relative to large populations, and vice versa for neofunctionalization. But they have no way of estimating or predicting the relative importance of sub vs. neo. It could be that neofunctionalizing mutations are 100 times more common than subfunctionalizing ones, even in small populations (and 1000 times more common in large populations). There is no theory (or data, really) that speaks to this.
May 28, 2015 at 1:04 pm
Devin Scannell
More than 3rd reviewer, thanks for your comments. A quick response.
1. Yes, there has been a lack of hygiene as regards terminology but I’d say it has not harmed the discussion.
2. Yes, my comment depends on the assumption that deleterious (partial) loss-of-function mutations (which can lead to subF/DDC) are more common than beneficial gain-of-fuction mutations (required for neoF)**. No question that the prevalence of duplicate preservation by neoF vs subF will be decisively influenced by these parameters, which are not well known. That said, mutation scanning experiments do tend to support the view that deleterious / LOF is more common than beneficial / GOF, as do mutation accumulation lines etc. Peter Keightley and friends – http://www.ncbi.nlm.nih.gov/pubmed/17637733
In any case, more experiments will decide this. Van Hoof looked at 4 out of ~600 duplicate pairs in S. cerevisiae. Lots more work to be done and plenty of opportunity for surprises. I have some fun ideas if anyone is interested 😉
** I am confounding functional and selective impacts of mutations here. mea culpa.
May 28, 2015 at 6:55 pm
More than 3rd reviewer
Hi Devin, it’s me, Matt Hahn (not sure why I chose the silly screen name, seemed appropriate last night). I agree that LoF mutations happen more often than GoF. However, DDC requires a first mutation that doesn’t abolish all function, then a second specific mutation that perfectly complements the functions abolished by the first mutation. My claim is that we still don’t know how often these happen.
June 4, 2015 at 3:21 pm
astoltzfus
Matt, that isn’t the case with the quantitative sub-functionalization model. There are a great variety of systematic mutation studies showing the prevalence of mutations that reduce activity partially. If you want to see an empirical distribution of reduction in activity, look at Fig 2 from Yampolsky & Stoltzfus, 2005 (http://www.genetics.org/content/170/4/1459.full.pdf).
The idea that a mutation would reduce protein activity partially is not at all surprising. The idea that a *second* mutation would reduce activity by y < x, where x is the degree of reduction of the *first* mutation, is also not at all surprising. That is the only condition of the quantitative sub-functionalization ("dosage") model.
June 4, 2015 at 3:31 pm
astoltzfus
sorry, made a mistake, let me fix that. In the quantitative sub-functionalization version of DDC, we start with twice the needed activity, and this is partitioned via fixation of neutral mutations so that neither copy is sufficient by itself, but the summed activity of the 2 copies is sufficient.
So, we start out with an activity of 2. If the first mutation fixed reduces activity from 1 to 1 – d1, the total activity is 1 + 1 – d1. Now the condition imposed on the second mutation (in the other copy), which reduces activity by d2, is that d2 <= 1 – d1. This will ensure retention, because each copy has activity = 1.
June 4, 2015 at 3:33 pm
astoltzfus
somehow my last sentence got distorted in uploading. Last sentence should be “This will ensure retention, because each copy has activity = 1”
June 4, 2015 at 3:35 pm
astoltzfus
hey, this interface is systematically doing some kind of substitution on my text!
One more time, without the symbols: “This will ensure retention, because each copy has activity *less than one-fold* but the pair together has activity of *at least one-fold*
June 4, 2015 at 5:49 pm
More than 3rd reviewer
Hey Arlin, good point. Quantitative subfunc should be easier to accomplish. Now if you ever find an example, let me know!
June 4, 2015 at 6:11 pm
astoltzfus
Matt, I’m not sure that I understand your skepticism. As I mentioned in another reply above, where I was complaining about how no one cites me for the quantitative sub-functionalization model, quantitative sub-functionalization is what Lan and Pritchard are arguing for in the paper that is the initial focus of this blog. So, if you want empirical evidence for an overall pattern that suggests quantitative sub-functionalization, it is there, and in the paper from Qian, et al. 2010 in Trends Genetics (http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2942974/). As I pointed out in 1999, there is a similar pattern (asymmetry in level consistent across tissues) in data on paralogous isozymes from the old days of molecular evolution.
I haven’t done a critical review of any recent evidence. I would be interested to know what others think of it. Probably there is a problem with not having predictions that are distinctive enough. If I had the bandwidth to work on this, I would be trying to make a more predictive model by leveraging some kind of quantitative model of the spectrum of mutational effects.
Or are you asking for a token case in which it is known with reasonable certainty that a particular pair of duplicate genes was retained via quantitative sub-functionalization?
June 4, 2015 at 6:19 pm
More than 3rd reviewer
Yes, I would like an example. Of course there are also no known examples of DDC as opposed to other subfunctionalization (as far as I know), so I realize it’s a high bar.
Also, since we’re deep into the ancient literature, Ohno clearly had some of the same ideas. See the section of his book on ‘‘The Differential Regulation of Former Alleles and Their Transformation to Isozyme Genes’’. I think the biggest difference is that you and Lynch proposed that the changes were non-adaptive.
May 28, 2015 at 3:41 am
Eric Lander
Thanks to all for the lively discussion!
As the senior author of the paper, I note that the framework for the analysis is stated in three consecutive paragraphs on p621 (reproduced below).
As stated in the first paragraph below, we were interested in seeing whether, for genes where duplication frees up at least one copy to evolve rapidly, the evidence better fits one model (“Ohno”: only one copy will evolve quickly) or an alternative model (both genes will evolve quickly). That is, the sentence at the end of the third paragraph below means “as opposed to the alternative model referred to above in which both copies would diverge more rapidly and acquire new functions.”
In this comparison, it is clearly “striking” (synonym: conspicuous), that the first model fits and the second does not – because, in examining those genes where at least one copy is free to evolve rapidly, you almost never see both copies evolve rapidly (that is, only 4 in 76 times).
Readers may differ as to whether this is the question they would choose to examine, but it’s the one that we chose to examine. I think the intended comparison is clear in context (as did the reviewers), but my apologies if it was not clear to all.
———————————————————————————————
Text from paper below:
“Two alternatives have been proposed for post-duplication divergence of duplicated gene pairs. Ohno has hypothesized that after duplication, one copy would preserve the original function and the other copy would be free to diverge1. However, this model has been contested by others, who argued that both copies would diverge more rapidly and acquire new functions20–22. We calculated divergence rates for the 457 pairs, using sequence information from K. waltii, S. cerevisiae and the related yeast S. bayanus (Fig. 4d). We searched for instances of unusually rapid or slow evolution.
We found that 76 of the 457 gene pairs (17%) show accelerated protein evolution relative to K. waltii, defined as instances in which the amino acid substitution rate along one or both of the S. cerevisiae branches was at least 50% faster than the rate along the K. waltii branch (Tables 1–3). We note that this calculation is conservative and may miss some cases of accelerated evolution (see Methods). These genes were heavily biased towards protein kinases (13 pairs, P-value 10-8) and regulatory proteins (8 pairs, including the cellcycle transcription factors Swi5 and Ace2, and the filamentation factors Phd1 and Sok2), and were generally involved in metabolism (38 pairs, P-value 10-18) and cell growth (32 pairs, P-value 10-10).
Strikingly, in nearly every case (95%), accelerated evolution was confined to only one of the two paralogues. This strongly supports the model in which one of the paralogues retained an ancestral function while the other, relieved of this selective constraint, was free to evolve more rapidly1.”
May 28, 2015 at 9:14 am
Joshua Plotkin
Thanks for joining the discussion, EL. Your comment highlights the essential issue underlying this “p-value problem”: the KBL analysis was designed to compare the Ohno and DDC models to each other, considering only those gene pairs in which “duplication frees up at least one copy to evolve rapidly”. The critical point is that the KBL analysis conditioned on at least one copy showing acceleration. A simple reading of the KBL text should make the intended comparison pretty clear.
Why, then, are many readers confused by this issue? In my case, at least, the confusion arose from the references cited in the first KBL paragraph quoted above (1, 20-22) and the preceding literature on duplicated genes. As they are typically described in the literature cited, the Ohno and DDC theories posit that _both_ copies of a duplicated gene are, by virtue of duplication, immediately free to evolve a new function and, in fact, that at least one copy (in the DDC theory, both copies) _must_ change functionality in order for both copies to be retained in the genome for a long time*. To compare either of these theories to data we should consider the patterns of evolution in all duplicate pairs retained in the genome, since the theory pertains to all such pairs. In other words, I would think that assessing the validity of either theory requires considering all duplicates retained, without conditioning on one or more copies showing accelerated evolution.
The consequence of this interpretation of Ohno’s theory, and how to test it, is clear: without conditioning, the natural null is independence, hence the majority of calculations seen in this discussion thread.
In retrospect it is clear what specific question was being analyzed by KBL. At the same time, that analysis does not seem to me as pertinent to evaluating evolutionary theories of gene duplication as alternative analyses that could be performed. Of course, post KBL there has been nothing to stop subsequent researchers from testing whatever theories of gene duplication they favor most, and however they see fit.
*The question how long qualifies as a “long time” is difficult, and problematic. Subsequent researchers have been surprised to find duplicates retained for tens or hundreds of millions of years without any detectible neo- or sub-functionalization in either copy, throwing doubt on both the neo- and sub-functionalization theories.
May 29, 2015 at 5:15 pm
striking
Reusing a metaphor proposed by two other commenters, defining a super-accelerated die one that returned a 6, we observe that out of all the pairs of dice returning at least a 6, only 1/6 contains another 6. I can’t wrap my mind about Profs Kellis and Lander trying to sell to a rational being, and less so to a mathematics professor, an irrational argument of this sort, albeit wrapped in lofty evolutionary jargon. I chuckle at the bio-purists calling for more experiments and “functional assays” to rectify the most puerile of statistical arguments. I can’t help but notice that the paper is peppered with p-values to support secondary claims, therefore the lack of a statistical assessment of an abstract level conclusion can only be deliberate. I’ve witnessed first hand the pressure exercised on analysis co-authors to support the “desired” conclusions, meaning publication-worthy findings. It’s no secret that reviewers for biology journals are mostly not even interested in the statistical, mathematical or computational aspects. I would suggest that the PI was a priori in favor of Ohno’s model, the data was not very forthcoming, the first author was interviewing including at the PI’s institution and it’s a time of your life when it’s hard to take a principled stand (it took me about 5 years of signing off misleading papers to look for a radical change — I am less successful, not any more pure than others). I was involved in one of the early ENCODE estimates of biochemical “function”. I’ve seen it change from 5% to 80% of the genome with no one even mentioning one of the old papers, and bemoaning the inconsistency. It had to be 80%, it had to support Ohno. My PI once told me, when I showed him our confidence intervals included his theory, the competing one and a few more: “then statistics must be wrong”. I don’t think he was downright dishonest: I think he was blinded by ambition and culturally impervious to mathematical reasoning, like many lab biologists. p-values were just one more obstacle, like publication fees, pesky reviewers, faulty reagents. Give me more data, make those equations disappear. It’s all arbitrary anyway, bayesian, frequentist, you can even swap the null and the alternative … He had no belief that statistics was the only way to make our statements stand the test of time. And if you look at the crisis of reproducibility across the biomedical sciences, this is not a Kellis or MIT or ENCODE problem. Who cares if some people believe in Ohno for another decade? I do, but it actually hurts more when it affects preclinical studies. Make no mistake, unless purifying selection is brought to bear on “striking”, irreproducible science on a urgent, radical basis, our departments will be so stocked with people just playing the game within a generation that only the appearance of Science will be left. Like ancient Roma senators who convened until the fall of the empire to support the illusion of a republic, we can have journals, grants, professors, editors, conferences and not have any Science, but only a shadow of it.
May 28, 2015 at 8:07 pm
Norman Yarvin
A side comment, as regards something quoted in the post:
…”the prevailing model for the evolution of gene duplicates holds that, to survive, duplicates must achieve non-redundant functions…”
Wait, what? Why can’t gene duplicates sometimes persist simply because more is better? Take the case of salivary amylase, where human populations with a longer history of eating grains have more copies of the gene for it. Is the prevailing model really to ignore such cases, and to insist that there are never situations in which more is better?
May 30, 2015 at 7:27 am
Manolis Kellis
Norman, our paper agrees with your point and concludes that the vast majority of gene pairs (321 of 457) lack accelerated evolution, at least with our stringent criteria, and that they may be retained due to altered gene regulation, or simply gene dosage.
The last paragraph is titled “Pairs with similar rates” and reads:
The remaining 321 of the 457 gene pairs did not meet our stringent criteria for accelerated or decelerated evolution. In some cases, the functional changes may be similar to those above but subtler. In other cases, the primary functional divergence may be in regulatory sequences. This seems a likely possibility because the extensive gene loss following WGD would probably juxtapose new combinations of intergenic and genic regions. In still other cases, the gene pairs may have been retained primarily to increase gene dosage, as with the slowly evolving genes.”
If one reads the original paper, you’ll see that we discuss several post-duplication fates, including:
* acceleration (76 pairs), where one copy accelerates in 95% of cases
* gene conversion (60 pairs), where copies have recently replaced each other (since S bayanus divergence)
* changes in codon usage (32 pairs), including cases where CAI is dramatically altered
* similar rates (321 pairs), which may simply reflect smaller acceleration, gene dosage, or altered regulation
I hope this helps!
May 28, 2015 at 8:26 pm
aNONymous
Could the 95% paralog pairs rate be compared to the empirical rates of accelerated evolution for random singleton pairs (pairs where neither genes have paralogs)?
My logic:
First, I imagined what would happen if there was NO duplication and this analysis was performed. All pairs of singletons (where at least one singleton needs to have a substitution rate of >50% as defined in the paper for “accelerated evolution”) would be compared and we’d know the fraction of singleton pairs that shows asymmetric accelerated evolution. This fraction can only be truly determined by counting because selection pressure most probably varies for different genes. Clearly, this fraction doesn’t mean much by itself. But it tells you the fraction if there were no duplications.
Now, introduce duplication into the picture. We want to know, reiterated again, if duplication and duplicate-retention drives asymmetric accelerated evolution. To do this, I would use pairs without any influence from duplication as a baseline control (ie. singleton-singleton pairs where at least one singleton has undergone accelerated evolution). If 0% of the singleton-singleton pairs showed asymmetric accelerated evolution, then the 95% paralog pairs rate would clearly be impressive and mean that the “paralog” status has special implications (namely that duplicates forces one paralog to resist evolving). But, if 95% of the singleton-singleton pairs showed asymmetric accelerated evolution, then the 95% rate for paralog pairs might not be due to the duplication — likely background since, here, most genes would tend not to undergo accelerated evolution regardless!
I think this comparison would allow you to either reject or not reject the Ohno hypothesis (which seemed to be the main hypothesis from the main text).
Sadly I couldn’t find all the data I needed from the supplementary to get a p-value…. 😦
Sidenote: Singletons could be binned based on annotated functions to control for variation in selective pressures based on them. Budding yeast is “fairly” well annotated.
May 29, 2015 at 11:11 pm
ianholmes
Tests based on rates have always seemed dubious to me. The rate is an artificial parameter and its maximum likelihood estimation introduces additional error. It would make more sense to formulate the test in terms of the actual data (i.e. observed substitutions), and integrate out any rate parameters as an unobservable nuisance.
Anyway, to summarize my impressions of this thread: you can get a hugely significant p-value with any null model that says homologous proteins should evolve at the same rate. That is a rather extreme choice of null model: independent rates would be more conservative. Yet that seems to be the gist of Lander and Kellis’ defense, i.e. that they were doing a model comparison and not (as Lior would like) a p-value test against a reasonable null model.
Model comparisons are fair enough, if they are understood as such. For example: “My mother thinks I am a legendary guitar player, my grandmother says I am a lazy goat. Strikingly, I do not have horns. This strongly supports the model that I am a rock god”
May 30, 2015 at 8:28 am
Manolis Kellis
Thanks for weighing in Ian and for your fabulous analogy. It seems that your grandmother’s hypothesis can be rejected with very strong statistical support, and that would be something to write home about. Our paper similarly was able to strongly reject the both-faster model, so we wrote home about it. Certainly, we could use other null models, but as i posted earlier, i have trouble with nulls that shuffle randomly between gene pairs blind to their function, so we focused on gene pairs, rather than single genes. We can keep debating this after 11 years, but I’m sure we all have much more pressing things to do (grants? papers? family time? attacking 11-year-old papers by former classmates? guitar practice?)
May 30, 2015 at 8:36 am
Michael Eisen
The more this conversation goes on the more it disturbs me. Lior raised an important point regarding the analyses contained in an influential paper from the early days of genome sequencing. A detailed, thorough and occasionally amusing discussion ensued, the long and the short of which to any intelligent reader should be that a major conclusion of the paper under discussion was simply wrong. This is, of course, how science should proceed (even if it rarely does). People make mistakes, others point them out, we all learn something in the process, and science advances.
However, I find the responses from Manolis and Eric to be entirely lacking. Instead of really engaging with the comments people have made, they have been almost entirely defensive. Why not just say “Hey look, we were wrong. In dealing with this complicated and new dataset we did an analysis that, while perhaps technically excusable under some kind of ‘model comparison defense’ was, in hindsight, wrong and led us to make and highlight a point that subsequent data and insights have shown to be wrong. We should have known better at the time, but we’ve learned from our mistake and will do better in the future. Thanks for helping us to be better scientists.”
Sadly, what we’ve gotten instead is a series of defenses of an analysis that Manolis and Eric – who is no fool – surely know by this point was simply wrong.
To me, their responses are more evidence that science in some quarters of our community has ceased to be a pursuit of new knowledge, and has instead become nothing more than a competition for points on the battleground of high-impact publication. If you are pursuing the truth, defending decade old statements that are clearly wrong makes no sense. It only makes sense if you view this kind of commentary as a threat not just to some long-buried asterisk on your CV, but to an approach to doing science that routinely produces this kind of “result”.
So I issue a challenge – or really a plea – for Eric and Manolis to stop being defensive and just admit they were wrong.
May 30, 2015 at 8:57 am
Michael Johston
For some reason, I never liked Manolis Kellis. Michael Eisen, your comments explain why.
May 30, 2015 at 9:48 am
anon
I’m surprised that this comment does not appear on the ‘recent comments’ thread. Was it added by the moderator?
May 30, 2015 at 9:52 am
Lior Pachter
There are sometimes delays in the posting of comments and their appearance in the sidebar. This must be some glitch in wordpress. For the record I, Lior Pachter am the moderator, and I have never posted any comments to any of the posts on my blog other than in my own name.
Also, for future reference you should know that WordPress records all IP addresses and displays them to the moderator, so that (a) you don’t have to take the moderators word when he says that “Michael” isn’t him as there is proof and (b) just because you post using the name “anon” with a fake email address doesn’t mean the moderator can’t know who you are.
May 30, 2015 at 9:03 am
Manolis Kellis
Mike, perhaps we can agree to disagree on that one. The evolutionary biology field is full of long-standing debates about mechanisms of neofunctionalization, post-duplication divergence, and other theories that are often hard to test. There are dozens of models proposed, with varying levels of simplicity, plausibility, or agreement with data. In this particular case, our paper conclusively showed that one of these models was inconsistent with our data, while another one remained consistent. 11 years later, the both-faster model remains unsupported by our data, and this was an important conclusion of our paper. You can call the alternative ‘asymmetric divergence’ or ‘independent divergence’, and i think both are fine, and they both continued to have both supporters and critics long after our paper. There is no underlying conspiracy here, our responses simply explain our modeling rationale. I hope this helps.
May 30, 2015 at 9:50 am
jchoigt
I see here an issue of fundamental scientific reasoning. Kelliis and Lander evidently conducted an analysis that disproved one hypothesis (that both copies of a duplicated gene will have similar rates of accelerated evolution) and then claimed the data supported another model (Ohno). I refer to Chamberlin’s 1890 paper on multiple working hypotheses and Platt’s 1964 paper on strong inference – science can properly disprove hypotheses, but it’s difficult to support any particular hypothesis unless you disprove all reasonable alternative hypotheses. So not having disproved the null model of independent evolution of duplicated gene pairs, the Kellis and Lander analysis cannot support any particular model.
May 30, 2015 at 11:54 am
Joshua Plotkin
As for the scientific issues in the thread, this comment from jchoigt really nails it. He reiterates more clearly and in greater generality the sentiments that others have expressed — about the perils of model comparison, and the need to reject all reasonable nulls in order to credibly establish a scientific hypothesis. I wonder what MK or EL really think about this point.
As for the meta-scientific issues, I am less pessimistic/suspicious than Eisen. I believe that the KBL authors sincerely believe their analysis is appropriate to conclude that their data are consistent with the Ohno theory, as the paper states. And so I feel there is value now, just as there was 11 years ago, in discussing the scientific merits of their argument.
May 30, 2015 at 12:38 pm
Joshua Plotkin
Edit: “to conclude that their data support the Ohno theory”
June 4, 2015 at 5:43 am
Erik van Nimwegen
Dear Joshua,
I admire your optimism but I think I agree with Mike Eisen on this, i.e. I am also surprised that the authors keep defending their interpretation.
Many people have pointed out that the 95% number is not ‘striking’, because this is what you would actually expect under a null model where ‘being accelerated’ is independent at each gene. To this the authors offer the defense that they only want to compare symmetric vs asymmetric acceleration models. But as many others (including you) have also pointed out, it is then technically incorrect to throw out all the pairs that came out as ‘both not accelerated’.
One might as well argue that, of the 376 pairs, a striking 80% (304) came out ‘symmetric’ (i.e. either both or neither accelerated), and claim that this provides support for the symmetric hypothesis. I think that this would be pretty much equally silly.
Moreover, from this thread I learned that somebody (the ‘names redacted’ comments that Lior posted) already informed the authors in 2004 that, not only is the 95% expected under the simple null model, but also that the evolutionary rates of paralogous pairs appear positively correlated in their data. This to me rather strongly argues that interpreting the data as rejecting the ‘symmetric acceleration’ in favor of the asymmetric model is not warranted. At a minimum one would have to devise a more informative test.
On top of that we now have the experimental data of van Hoof, and the papers of Pritchard and from the Petrov lab that Lior discusses, which all further cast doubt on the asymmetric acceleration model.
Given all this information, I am also surprised that the authors apparently still believe that their data rejects symmetric acceleration and strongly favors the assymetric acceleration model.
From a perspective of ‘scientific progress’ I agree with Mike that it would be helpful if the authors would simply admit that, in hindsight, they agree their data should not be taken as strong evidence for the asymmetric acceleration model over the symmetric acceleration model.
June 4, 2015 at 9:54 am
ot
Erik, I am afraid you interpret “symmetric” evolution wrong. Kellis said symmetric means only both copies accelerated, excludes the case that neither copy accelerated. Symmetric evolution is actually extremely unlikely. If you look at 83%, the percentage of pairs which are both not accelerated, this is a very high fraction, significant probably by any statistical test. Thus, while we keep talking about the 76 pairs, let’s not forget that the remaining 83% of pairs are also quite significant. There is no doubt in my mind that Kellis’ observations couldn’t have arised by random chance.
June 4, 2015 at 12:35 pm
Erik van Nimwegen
Dear ot,
I’m afraid you missed the point I was trying to make. Your reply made me realize that others may also miss it, so let me try again.
KBL defined ‘accelerated evolution’ in such a stringent manner that only a small fraction of all genes are classified as ‘accelerated’. That is among the 457 analyzed pairs, only 76 pairs have at least 1 adhering to this definition, and only 4 have both paralogs as accelerated. The key point is that, with these numbers, if you pick a random gene from a pair, the chance that it will come out as ‘accelerated’ is (76+4)/(2*457) = 0.086. If you now ask: what is the chance that the second gene of the pair is also accelerated it is 8/80 = 0.1. So if anything, observing the first gene accelerated makes the second in the pair more likely to be also accelerated. But given the relatively small numbers involved, there is really no significant difference between these empirical percentages.
In summary, the data says that, given that the first gene is accelerated, the second gene is neither more nor less likely to be accelerated.
So, at least based on this simple binary feature of being either ‘accelerated’ or not (as defined by KBL), the data does not ‘strikingly’ favor either symmetry or asymmetry. Suggesting otherwise is really just a mistake in my opinion.
This doesn’t mean that you cannot cook up a percentage that makes it appear, at first blush, to support either symmetry or asymmetry. You presumably know the famous quote: There are three sorts of lies… Lies…damned lies…and statistics.
Focusing only on the 76 pairs that have at least 1 accelerated gene leads to a misleading statistic (the 95%) that erroneously suggests the data strongly support asymmetric evolution. My example was just to show that, if one slightly redefines ‘symmetric evolution’ to mean: both genes do the same (i.e. either both accelerated or both not accelerated) then you can get an equally misleading statistic suggesting that the data suggests ‘symmetry’. But as I pointed out, that would be an equally silly thing to do as focusing on only the 76 pairs where at least 1 one was accelerated.
June 5, 2015 at 3:02 pm
Manolis Kellis
Dear Erik, thanks for weighing in. I know you can’t keep up with every comment in this blog, but I believe my comment to Pavel and his class on June 3rd will help clarify the issues that you’re bringing up https://liorpachter.wordpress.com/2015/05/26/pachters-p-value-prize/#comment-4436 I can expand on it briefly here.
As I write in my comment, we were quite clear about the two models our paper was comparing and the specific approach we took to compare them. We compared Ohno 1970 vs. Force 1999’s critique of Ohno, and we found that we could reject Force’s critique, but that Ohno was consistent with our data. We thus argued in favor of the original model rather than the revised model.
(Of course, subfunctionalization is still a very attractive model for large genomes with small effective population sizes, as it does not require any beneficial mutations, does not rely on gene dosage, and could allow for >70% duplicate gene preservation. In yeast, a small genome with a population size estimated to 7-8 million in Europe (Tsai 2008), selection seems to act effectively enough that beneficial mutations can indeed be fixed)
——–
Expanding on point (1) of my comment https://liorpachter.wordpress.com/2015/05/26/pachters-p-value-prize/#comment-4436 our disagreement seems to stem from two parallel interpretations of Ohno 1970. (a) Our paper’s interpretation is that “*only a subset* of genes will show accelerated evolution, but that those that do, will do so asymmetrically”. (b) The interpretation provided by you, Mike Eisen, and Joshua Plotkin is that *every* gene pair should show asymmetric acceleration.
However, Part 3 of Ohno 1970 proposes multiple scenarios for duplicate preservation in chapters X-XIV. The first scenario is gene dosage and gene conversion (no acceleration), the second is heterozygous advantage by maintenance of both alleles (no acceleration), the third is differential regulation (no acceleration), and only the fourth is gain of new functions (acceleration). Thus, not every pair should show acceleration, but the ones that do should do so asymmetrically.
Somewhat at odds with Ohno’s writing, Force 1999 states that “under the model first elucidated by Ohno (1970), the only mechanism for the permanent preservation of duplicate genes is the fixation of rare beneficial mutations endowing one of the copies with a novel function” (p.1532), and “the most basic premise of the classical model of duplicate gene evolution – that gene duplicates are preserved only by the evolution of gene functions” (p.1542).
Force 1999 is also somewhat at odds with Ohno’s original writing even when describing how new functions arise under Ohno’s model. Ohno writes that “the first forbidden mutation” results in “the production of a useless polypeptide chain” and that “natural selection would ignore the redundant locus, and thus, it is free to accumulate a series of forbidden mutations” and “might finally acquire” a function (p. 72). In contrast, Force write that “neofunctionalization relies entirely on rare beneficial mutations” (p. 1543), and that their model “is quite distinct from the classical model, under which degenerateive mutations can only lead to gene loss and beneficial mutations are the only route to gene preservation” (p. 1533).
This partly incorrect interpretation of Ohno 1970 may be at the heart of our debate. Indeed, if Ohno had described his model the way that Force 1999 quotes it, we would predict that every gene pair must show accelerated and asymmetric evolution. But the way that Ohno 1970 described his own model, we predicted that many genes do not need to show accelerated evolution (Chapters X, XI, XII), and only a subset will do (Chapter XIII). However, for that subset, we would predict asymmetric evolution.
——–
Point (2) of my comment to Pavel and his class ( https://liorpachter.wordpress.com/2015/05/26/pachters-p-value-prize/#comment-4436 ) addresses the model of independence, which was not considered in our paper, but has been proposed by many in this conversation as fitting the data equally well.
Even though independence hasn’t been formally proposed as a model of post-duplication evolution, proponents of this model argue that each copy in a gene pair would evolve independently, and that this is also consistent with the fraction of accelerated gene pairs.
However, the independence model makes a very strong prediction that if copies in duplicated gene pairs evolve independently, then gene loss would have actually occurred at random, which is simply not the case.
Instead, we find that 90% of genes in doubly-conserved synteny (DCS) regions are preserved in at least one copy, and that only 12% are preserved in both copies (see http://www.nature.com/nature/journal/v428/n6983/extref/S5_Poster/all_scaffolds.pdf ).
The independence model would predict that only 75% of genes would be preserved in at least one copy, and that 26% would be preserved in both copies, which is strongly rejected by a chi-square test given the hundreds of genes in each category.
——–
Certainly, we can debate many additional aspects of post-duplication evolution, and they are fascinating. However, our paper made a simple model comparison between Ohno and its criticism by Force. Still worth reading the originals though, as there’s still a lot of material for debate, and these are very interesting questions to debate
June 6, 2015 at 2:26 pm
Erik van Nimwegen
Dear Manolis,
thanks for your response to me. I understand that not all pairs will need to show either symmetric or asymmetric acceleration. But I do maintain that it is simply incorrect to perform a statistical analysis only on the set of 76 pairs for which at least 1 happens to pass your cut-off for ‘acceleration’ without failing to take into account that, for 381 pairs, neither gene passed the cut-off. I gather this point is still not clear so I will give another try explaining it.
Let’s first note that the data of evolutionary rates doesn’t look anything like a bimodal distribution where some genes are clearly accelerated relative to the branch without duplication, and some genes are not at all accelerated. Instead, there is pretty much a continuous distribution of rates, with different genes showing more or less acceleration or deceleration. Given this, picking a fairly arbitrary cut-off on relative rate and using this to classify genes as ‘accelerated’ or ‘not accelerated’ is clearly throwing away highly relevant information. Moreover, neither of the models you wish to compare make any clear predictions about how much the rates must be accelerated or differing, and so, whatever cut-off you pick, you are likely to miss cases where genes were really accelerated but did not pass the threshold (especially when you pick a stringent threshold), and you may call genes as accelerated that really weren’t (especially at a low threshold). Moreover, one could easily see that the the probability of ‘missing’ symmetric and asymmetric cases is not the same, thereby introducing systematic biases. So at a minimum I would want to check how the results depend on the cut-off.
In any case, with your cut-off, the numbers you get say that the probability for one gene in a pair to pass the cut-off is independent of the probability that the other gene in the pair will pass the cut-off. So your data strongly suggest a simple model in which the probability for genes in a pair to pass your acceleration cut-off is independent.
So what’s wrong with such a simple model?
You seem to imply that such a model must then necessarily also predict that genes in a pair should be independent in ALL respects, including having independent probabilities of being lost. I do not understand why you think that this follows. All the simple ‘independent’ model has to assume is: the evolutionary behaviors of genes in a pair is variable enough such that the probability of passing the KBL-acceleration-cut-off is pretty much independent for the two.
That certainly seems like a very simple model to me and the data perfectly fits it. I have not seen any coherent objection to it.
In contrast, it seems to me you want to use the following reasoning:
-The fact that only a fraction f(acceleration) = 80/914 of genes show acceleration according to a fairly arbitrary cut-off should be interpreted as saying ‘true acceleration’ is rare, i.e. it happens in a fraction f(acceleration) of all genes.
-Among the 76 ‘truely accelerated’ pairs, there are only 4 double accelerated pairs. This should be interpreted as saying that, whenever there is ‘true acceleration’, this acceleration is asymmetric 95% of the time. Or to put it differently, you find f(asymmetric|acceleration) = 0.95
But note that, under this reasoning, there is no reason whatsoever to expect that there should be any relationship between f(acceleration) and f(asymmetric|acceleration). However, we find that the fraction of pairs with both genes accelerated is ALMOST EXACTLY f(acceleration)^2.
In your interpretation, this is just coincidence. That is, the fact that the ratio p(second in pair accelerated|first in pair accelerated)/p(first in pair accelerated) is almost exactly 1, is just a big coincidence.
Now, although I find it quite ‘striking’, it might be coincidence of course. So I wondered to what extent this depends on the chosen cut-off. If you are right and it really is coincidence, then I would expect that
f(assymetric|acceleration) is insensitive to the cut-off, whereas the observation p(second in pair accelerated | first in pair accelerated)/p(first in pair accelerated) = 1 should be a coincidence that only happens for the specific cut-off 1.5
So I downloaded the supplementary table and checked how the various statistics depend on the cut-off. What I see is almost exactly the opposite.
The fraction f(assymetric|acceleration) is highly dependent on the cut-off. When then cut-off is 0.8 it is 23%, at 1 it is 57%, and at 1.2 it is 89%. In fact, this fraction always closely follows the overall fraction of genes that are called as accelerated. In contrast, the ratio p(second in pair accel| first in pair acel) is always close to one (it ranges between 1 and 1.4 as the cut-off varies from 0.4 to 1.6).
So the observation is: how many genes get called as accelerated depends strongly on the cut-off, but it is always true that the chance of the second gene in a pair being called as accelerated is independent of the first gene being called as accelerated.
If you still think that this is all just coincidence, and that a simple independence model should be rejected over a more complicated interpretation in which certain fractions happen to consistently match by accident, then I think I will give up.
May 30, 2015 at 9:53 am
Justin Fay
Previous posts assume that the power to detect accelerated genes is 1 and that the rate of false positives is 0, both of which are unlikely or at least unknown.
The null model is that pairs are either both accelerate or not. The alternative is that only one gene of a pair is accelerated.
M = # accelerated pairs
N = # non-accelerated pairs
(Under the null model there are no cases where one gene of a pair is accelerated)
If q is the power of detecting an accelerated gene, then:
q = 1, 72/76 is strikingly significant.
q = 80/914 (minimum value of q) then previous comments are correct and it is not.
If p is the rate of detecting an unaccelerated gene (false positive), then:
p = 80/914 (maximum value of p) then the observation is not striking.
TP = The expected number of true positive accelerated pairs = M * q^2
TS = The expected number of true pairs where only one detected as accelerated = M * 2 * q * (1-q)
FP = The expected number of false positive accelerated pairs = N * p^2
FS = The expected number of false pairs where only one detected as accelerated = N * 2 * p * (1-p)
The probability under the null model is thus:
cdf binomial with 4 successes, 76 trials, prob. success = (TP + FP) / (TP+TS+FP+FS)
Although we know TP+TS+FP+FS = 76 and M+N = 457, we don’t know p or q.
If q is close to one and p is close to zero, striking is justified, otherwise it is not.
May 30, 2015 at 10:25 am
Marnie Dunsmore
What’s with Kellis’ use of hyperbole in so many of his statements (see above) ?
” we find astronomical p-values for 72 of 76 pairs being asymmetric.”
“it’s hugely significant”
“In a likelihood ratio framework, the Ohno model is 10^87 times more likely, leading to significant rejection of the BS null, and a cash prize of 903,659,165 million billion trillion quadrillion quintillion sextillion dollars, which LP can choose to award in 2015, 2004, 1970s, or 1930s dollars.”
Sextillion.
“Moreover, we infer that along with possibly gaining a new function, the derived copy has lost some essential aspect of its function, and cannot typically complement deletion of the ancestral gene.” This is completely consistent with the subsequent experiments.”
Completely consistent.
“Thanks for weighing in Ian and for your fabulous analogy. It seems that your grandmother’s hypothesis can be rejected with very strong statistical support, and that would be something to write home about. Our paper similarly was able to strongly reject the both-faster model, so we wrote home about it.”
Fabulous analogy.
These hyperbolic comments are not the only ones that Kellis engages in. His press statement in Science Daily seems rambling and a little bizarre:
http://www.sciencedaily.com/releases/2004/03/040308071448.htm
Sure, he’s not the only one that uses this kind of language, but to me anyway, it makes him sound more like a used car salesman than a scientist.
Regarding the p value calculation, like many other people have pointed out, the null hypothesis should show the degree to which protein acceleration occurred in the “background” total gene pool. Intuitively, it appears that protein acceleration can appear in both singletons and gene pairs. Judging by many of the comments, there are many assumptions that come into establishing what the “background” protein acceleration picture looks like.
I guess I will get on with reading the Lan and Pritchard paper.
May 30, 2015 at 10:49 am
Manolis Kellis
Oopsy, thanks for pointing it out Marnie. I usually try to watch my language, and be a little more restrained and less emphatic in my posts. In your examples, the simple test is indeed hugely significant, sextillion is indeed a word, and the experiments are indeed completely consistent. But I could have found a better word to describe the analogy (“flowery” was a close second). It’s finally Spring in Boston, so everything seems fabulous around here, but i’ll try to curb my enthusiasm for scientific arguments
May 30, 2015 at 7:18 pm
mamba_stats
Statistically significant doesn’t really mean scientifically significant, especially when your null is incorrect. I also think the critic on “sextillion” and “fabulous analogy” words is a bit unfair. But to me “hugely significant” and “completely consistent” are just hyperboles
May 30, 2015 at 9:02 pm
mjcgenetics
Thanks go to my ninth grade biology teacher, Mr. MacDonald.
If this wins a prize, please donate it to the Conquer Cancer Foundation in the names of Lin Patch and Adam Balch. Thanks.
May 31, 2015 at 6:53 am
mjcgenetics
It strikes me (hah!) that, reading the statement in question again (“Strikingly, 95% of cases of accelerated evolution involve only one member of a gene pair, providing strong support for a specific model of evolution, and allowing us to distinguish ancestral and derived functions.”), I realize now why Manolis used the term “strinkingly”–his null hypothesis was actually different from that which I used in my hotel floor calculation last night. Here is what I think he was referring to:
H0 = S. cerevisiae = 4/76
H1 = S. cerevisiae = 76/76
X^2 = 17.05
DF = 1
p-value < 0.01 (i.e. "striking")
Of course, this whole discussion points to one major thing: It is important to be explicit about what statistical tests are being used to make statements, particularly when they involve words that may be misconstrued as hyperbole.
I recently received back a paper with a criticism from a reviewer referring to a section that went to great length to describe in detail the statistical tests used to make various statements in the manuscript which said, and I quote: "statistics should be self-explanatory".
But that's the thing about statistics. They aren't self-explanatory. You need to explain what exact tests you used so the rest of the field can assess whether it was an appropriate test.
To quote a statistician I trust very much: "I can give you any p-value you want. The question is actually which test you use to determine it."
May 30, 2015 at 9:32 pm
Tau-Mu Yi
I will address the bonus question. From the perspective of a yeast biologist and the yeast biology community, we were mainly interested in “Proof of WGD in S. cerevisiae” i.e. Figs. 1-3. This alone is worth the price of admission IMO. Many of us work on one or both genes of a homologous pair, and at some point we need to explain why there are 2 genes: WGD. This use-case probably represents a fair fraction of the 1000 or so citations.
Because of the Kellis et al. paper I always favored the neo-functionalization model without really spending time thinking carefully about it. This blog post has rectified this gap in my understanding.
The responses above of Manolis and Eric make sense to me: they did the test they explicitly stated in the paper, although perhaps not the one a lazy reader (i.e. me) might have assumed. Perhaps I should have read certain passages in the paper more critically, and perhaps the editor and reviewers should have done so too.
For certain, the editor at Nature who did not print the rebuttal letters should be reprimanded.
I would like to thank Lior for raising this issue and conducting the discussion in a reasonably professional manner. I also would like to thank him for reminding me that I need to cite Kellis et al. (2004) in the manuscript I am working right now from which I am taking a procrastination break to type this reply.
May 30, 2015 at 9:47 pm
Pavel Pevzner
Thank you Eric, Lior, Manolis, and everybody who provided comments on this blog. The KBL paper is now textbook material: just two weeks ago, we taught it to 1000s students in our Coursera “Bioinformatics Algorithms“ class (http://coursera.org/course/bioinformatics2), and there will be a section on KBL in the 2nd volume of our “Bioinformatics Algorithms” textbook (http://bioinformaticsalgorithms.org) to come out in July 2015.
In view of the discussion here, I and my co-instructor Phillip Compeau have decided to make a break in the Coursera course and to ask students to spend a week reading KBL and related papers, thinking about the posts on the blog, and perhaps even submitting solutions for the P-value prize challenge 🙂 We have excellent students: 13% of them hold Ph.D.s, and 34% hold M.S. degrees. I hope they will contribute to the discussion in a meaningful and CONCILIATORY way. Even more importantly, I hope they will learn that they should be skeptical and double check everything I tell them in class.
Thank you again for providing a great learning opportunity for our students!
May 30, 2015 at 11:53 pm
Lior Pachter
Thanks Pavel and Phillip. I’ve extended the deadline for the prize by a week to accommodate students from your class. They are welcome to post comments and/or submit entries.
May 31, 2015 at 9:43 am
oriental
I agree that the last sentence of the abstract is misleading and should be improved. On the up side, the paper was considered novel and revolutionary at the time. Here is my solution, which does not report p-values, since further information would be needed, but helps you see at least that asymmetric evolution is preferred over symmetric evolution, given the information presented in the post.
Let (0, 0) be the event that a pair has no accelerated evolution in either copy.
Let (1, 1) be the event that a pair has accelerated evolution in both copies.
Let (0, 1) be the event that a pair has accelerated evolution in one copy only.
We condition on the fact that 381 of 457 pairs have no accelerated evolution in either copy. Thus, P(0,0) = 0.83
This means that P(0,1) + P(1,1) = 0.17.
We wish to test two models of evolution to see which one can explain the observed statistics:
one is asymmetric evolution (P(0,1) + P(1,0) > P(1,1)), and we can assign some hypothetical probability of 0.90 to favor this over the other. (so P(0,1) = 0.90 * 0.17, P(1,1) = 0.17 – P(0,1)))
the other model is symmetric evolution (P(1,1) > P(0,1) + P(1,0)), and we can give it some hypothetical probability to favor this event (P(1,1) = 0.90 * 0.17, P(0,1) = 0.17 – P(1,1))).
Then given the observation of 72 pairs (with one copy accelerated), and 4 pairs (with both copies accelerated), the probability of this observation can be summarized using the 3-outcome model (based on changing the binomial probability to use 3 outcomes rather than 2):
prob = 457! / (381! 72! 4!) * p^72 q^4 (0.83)^381
where p = P(0,1), q = P(1,1), p+q = 0.17
In the asymmetric case, plugging p = 0.90 * 0.17, q = 0.17 – p, gives the overall prob of 0.003.
In the symmetric case, plugging p = 0.10 * 0.17, q = 0.17 – p, gives the overall prob of 4.12e-68.
In the case that both models are equally likely, plugging p = 0.5 * 0.17, q = 0.17 – p, gives the overall prob of 8.3e-19.
So asymmetric case has the best chance (of the two) of explaining the observations, where the other ones are extremely unlikely to arise by random. All still have low probability, suggesting that actual observations are non-random, but first one is closest to being explained by a random model. You can substitute hypothetical 0.9 with other reasonable values you like and you will come to the same conclusion.
June 1, 2015 at 11:14 am
homolog.us
Here is my entry. The figures are visible in the blog post (http://www.homolog.us/blogs/blog/2015/06/01/breakdown-of-trust/), but we would love to attach them here [ed: they have been included in the comment below].
Bioinformatics for Married Couples
Our recent research uncovered new principles at the interface of evolution and psychology that will lead to better understanding of marriages. Therefore, we are submitting it to the most visible journal, which happens to be Lior Pachter’s blog.
Many American marriages end up in divorces. A Japanese-American scientist noticed the rising trend in 1970 and explained it based on socio-evolutionary theory in his book. He suggested that man, being a solitary animal, does not like to remain paired and that is the reason for the rising trend.
His model was never tested experimentally, but due to availability of large-scale analysis tools, we were able to do that in our lab. We conducted an experiment, where we placed 457 married couples (457*2 persons) in a room and picked 80 persons using an elaborate pipeline developed by us (see attached script). Strikingly, in 95% of cases (72/76), we got only one member of the couple and not the other, supporting the theory of mentioned Japanese scientist.
#!/usr/bin/perl
#
# put 457 married couples in a room
#
# each member of a couple is assigned a number
#
for($i=1; $i<=457; $i++)
{
push @room,"HUSBAND$i";
push @room,"WIFE$i";
}
#
# pick 80 persons randomly
#
$N=@room;
for($i=0; $i<80; $i++)
{
#
# randomly pick a person
#
$pos=rand; $pos=int($pos*$N);
#
# find the number on it
#
$selected_person=$room[$pos]; $selected_person=~s/HUSBAND//; $selected_person=~s/WIFE//;
# keep count
$count{$selected_person}++;
}
#
# how many of those 80 will be couples?
#
$same=0;
foreach $key (keys(%count))
{
$same++ if($count{$key}==2);
}
print "$same\n";
The above script randomly picks 80 persons from a pool of 457*2. You can see the distribution of number of pairs in the following figure that is generated by running the script 10000 times:
June 1, 2015 at 9:06 pm
Brian Raney
If I learned anything in grad school it was that without a prior expectation, likelihoods mean nothing. For example, my prior expectations of pvalues that are less than the reciprocal of the estimates of the total number of atoms in the Universe (~1e80) suggest to me that the method by which the pvalue was calculated was using a model that was lacking the ability to capture the Universe in a significant way, regardless of the hypothesis.
June 1, 2015 at 10:16 pm
Pavel Pevzner
With all due respect, imposing a lower limit on p-values based on the number of atoms in the universe is a pseudo-statistical folklore. Take a look at the celebrated work by Ted Harris on neutrinos trying to make it through the concrete slab (from 1951!) to realize that p-values can go as low as they wish with increase in the width of the slab. If you want a more biological example, take a look at p-values of Protein-Spectrum Matches in top-down proteomics to see that just 70-80 fragment-ions in a spectrum of a short protein can make p-values go below what Manolis has suggested. And people in top-down proteomics routinely report very low p-values in their papers. So, unfortunately for Lior and his family, there is really no upper limit for the P-value prize…
June 2, 2015 at 7:49 am
D. Allan Drummond
We don’t need to enter reciprocal-of-particle-counts territory, folklore or not. A printed p-value becomes meaningless when it is substantially exceeded by the probability that the p-value contains a typo.
June 2, 2015 at 10:58 am
Pavel Pevzner
Sure. And to account for the likely typos, each time you write a p-value on a piece of paper, don’t forget to adjust it depending on how many shots of vodka you had the night before.
June 3, 2015 at 2:40 pm
tt
Strikingly, Lander was on Pachter’s PhD thesis committee
June 5, 2015 at 11:50 am
psuedo is ver2
RE: the post by tt at June 3, 2015 at 2:40 pm
I first thought it was a joke. After a while, I’m curious to check it out how it holds up.
After I checked with Lior Pachter’s CV, which listed Lander as his co-advisor.
Then I found Lior Pachter’s thesis at http://dspace.mit.edu/bitstream/handle/1721.1/85308/43855315-MIT.pdf?sequence=2
Unfortunately, Lior Pachter’s dissertation didn’t list his thesis committee, so it is hard to verify whether Lander was actually on his thesis committee. Maybe someone else can find out more than what I can, or maybe Lior Pachter can speak for himself.
June 5, 2015 at 11:54 am
Lior Pachter
I was a graduate student at MIT where Bonnie Berger was my official advisor. However during my Ph.D. I worked closely with Eric Lander to the extent that I consider him to have been my informal co-advisor. He was also on my thesis committee. He was an excellent mentor and a fantastic professor to work with. I don’t see how any of that is relevant to the present blog post.
June 5, 2015 at 12:07 pm
psuedo is ver2
The post gets too deep to be nested. This is a reply to Lior Pachter at June 5, 2015 at 11:54 am
Thanks for the confirmation. The tt’s original post just brings up my own curiosity. Of course, this digressed discussion has nothing to do with the current scientific discussion per se, but it will be interesting to see how the people are connected with you in you blog.
On this blog, I admire that you can criticize any paper, no matter how connected you are with the author, regardless of being a friend or a foe.
June 3, 2015 at 6:56 pm
Manolis Kellis
Dear Pavel, Thank you for bringing your class into this debate. I will try to summarize and parse some of the points in the discussion.
The quoted sentence of our paper addressed the following question:
* Ohno had proposed that new gene functions would evolve asymmetrically, with one copy preserving the old function, leaving the other copy free to take on a new function.
* Force et al. proposed an alternative model whereby both gene copies would be relieved of selection symmetrically, taking on subfunctions of the original function.
* To distinguish between these two models, we focused on the 76 pairs that show acceleration, and found that 95% are accelerated in only one copy.
* This argues against Force’s critique of Ohno.
Our paper was clear about both the specific question asked (Eric’s post cites the relevant text) and the answer obtained.
The comments on the blog largely focus on two additional questions that weren’t studied in our paper. Still, it’s worth taking a moment to discuss them:
(1) ME and JP interpreted Ohno’s model as predicting anti-correlated rates for all gene pairs (which is different than our understanding of Ohno’s model). This interpretation may be due to the fact that Force describes Ohno’s model as: “the only mechanism for the permanent preservation of duplicate genes is […] endowing one of the copies with a novel function”. Notably, Ohno did not actually say this. Rather, Ohno 1970 proposed multiple mechanisms for maintaining duplicated genes – including gene dosage and gene conversion (chapter X), heterozygous advantage by fixation of two alleles (chapter XI), differential regulation (chapter XII), and new gene functions (chapter XIII) which ‘might finally’ arise. Thus, Ohno’s model (at least as Ohno described it) does not predict anti-correlated evolution for all preserved gene pairs, but merely that those pairs that show acceleration will tend to do so asymmetrically.
(2) LP and (names redacted) comment that we did not consider an alternate model (“independence”) whereby each copy of a duplicated gene would evolve independently, without regard to the function, preservation, or evolutionary rate of the other copy. Indeed, we didn’t consider this model (or many other models, for that matter). However, it’s worth noting that the independence model is not biologically rooted and is inconsistent with our understanding of post-duplication selective processes. In particular, independence predicts that gene loss would occur at random after whole-genome duplication, rather than in the highly coordinated manner observed. In particular, 90% of K. waltii genes are maintained in at least one sister region, and 12% are maintained in both copies, indicating selective pressure to maintain at least one gene copy despite a 49% loss rate for individual gene copies. Given this loss rate, independence would predict that 26% of genes would be kept in both copies (0.51^2), 24% of genes would be lost in both copies (0.49^2), and the remaining 50% in a single copy, which is highly inconsistent with the data. Given the very large gene counts, a two-way contingency table results in a chi-square statistic of x^2=827 with DF=2 degrees of freedom (P<10^-100), indicating that independence can be rejected with very strong statistical support.
In any case, there remain many interesting questions about the behavior of genes after whole-genome duplication.
June 3, 2015 at 7:17 pm
Lior Pachter
Dear Manolis,
In your comment you say that “LP and (names redacted) comment that we did not consider an alternate model…” I’m not sure if by LP you were referring to me, but since my initials are in fact LP (for Lior Pachter) I just want to note that nowhere on this blog post have I commented about your paper (and than to post comments of others who wished to be anonymous), and I certainly haven’t suggested you should have considered an alternate model. I will post my own thoughts about the paper and what I think you should or shouldn’t have considered when I announce the prize winner on Monday.
Thanks,
Lior
June 3, 2015 at 8:16 pm
Pavel Pevzner
Since some Coursera students have already noticed that the discussions on this blog are rather heated, I thought I should try to explain to them that bioinformaticians are nice people rather than a mean-spirited bunch 🙂
Dear students, computational folks sometimes take biological papers a bit too seriously. IMHO, many papers on molecular evolution are merely short novels (published in journals like Science and Nature that general audience don’t care about) rather than rigorous “proofs”. Some people try to keep these short stories to the standards of “Annals of Statistics” but this is a futile exercise in a community where only a fraction of biologists know what the null hypothesis is and can say what is the difference between the P-value, E-value and FDR. For many, these values are just annoying obstacles to be navigated before a paper is submitted. Excuse me for being cynical here and below.
The real measure of success for a novel is whether it was “bought” (i.e., accepted and widely cited) by thousands of biologists. Or bioinformaticians like me who believe that KBL is a very interesting novel – I even published papers elaborating on KBL and have been presenting parts of KBL in my classes.
Bringing up the issue of P-values to evaluate a best-selling novel is unusual – nobody judges Daniele Steele’s novels by Chekhov’s standards. And as in every novel, the choice of specific metaphors (like “Strikingly” or “Proof”) is solely at the discretion of authors – any opinion otherwise is an attack on freedom of speech.
I learned it the hard way when I wrote a letter to Science on exactly the same topic (computing P-values) in a different context – raising a doubt about sequencing T. Rex proteins. Needless to say, Science did not want to publish it (who cares about P-values when the story is on all TV channels!) until personal intervention of the Editor-in-Chief who insisted that the letter should be published (http://www.sciencemag.org/content/321/5892/1040.2.long).
In summary, I think this post, while entertaining, is discussing an extremely narrow issue. IMHO, KBL is a good paper that, undoubtedly, like most Nature/Science evolutionary novels, has some issues and that indeed may have used some excessive metaphors. So what? Can one even make it to Nature/Science without using this lingo? I am fine with “Strikingly” since there are various interpretations of the null hypothesis. However, I get nervous when the word “PROOF” (that appeared in the KBL title) shows up in any paper on evolution. If it is a “PROOF”, why the paper by Wolfe and Shield, Molecular EVIDENCE for the duplication of the entire yeast genome. Nature 1997 is not an even earlier proof of WGD? Or does “EVIDENCE” have a larger P-value than“PROOF” 🙂
To further elaborate on my attitude towards “Proofs” and “P-values” in evolutionary studies, I want to remind the students the following paragraph from Lesson 6 in our Coursera class commenting on yet another controversial conjecture by Ohno (page 292 in Compeau and Pevzner. Bioinformatics Algorithms: An Active Learning Approach. 2014):
[…we will never be able to prove a scientific theory like the Fragile Breakage Model in the same way that we have proved one of the mathematical theorems in this chapter. In fact, many biological theories are based on arguments that a mathematician would view as fallacious; the logical framework used in biology is quite different from that used in mathematics. To take an historical example, neither Darwin nor anyone else has ever proved that evolution by natural selection is the only—or even the most likely—explanation for how life on Earth evolved!]
The last sentence will likely be viewed as heretical by many biology professors but, in a free country, there is nothing they can do to stop us.
For me, a bigger issue wrt the P-value prize controversy is EDUCATION and a great opportunity for students to see an unfolding debate involving top people in bioinformatics. A lesson is that biologists should be trained to be computationally skeptical and computational culture should become a job requirement for Nature/Science editors and reviewers. This requires a revolution in computational education of biologists and it has a long way to go: the biology graduates today are not prepared to the computational challenges of their own discipline… While you are reading this blog, think what fraction of biologists (the intended audience of KBL) can even follow the logic of various entries for the P-value prize.
I know that both sides of this discussion are deeply involved in computational education of biologists and lead efforts towards improving it at their institutions. There is a long way to go. Lior, our daughter, who graduated with honors from YOUR UNIVERSITY in Biology three years ago, just finished the first year of medical school and returned back home. Eric and Manolis, after finishing Berkeley, she worked for two years at YOUR INSTITUTE and published great papers in PNAS and PLOS Biology. So I asked her at dinner “Do you know what the P-value is?” She responded “Yes.” I thus asked her “What is it?” and she responded: “It should be smaller than 5%.” I checked one of her papers and it indeed presents various P-values that are all smaller than 0.05! PHEW.
If the number of hits to the P-value page on Wikipedia has increased in the last week, Lior is to blame. But how many biologists can compute the P-value for this increase??? If I had any influence on the P-value prize decision I would award it to LP and KBL for a good discussion and for making biologists aware that P-values matter!
June 3, 2015 at 9:28 pm
homolog.us
“To take an historical example, neither Darwin nor anyone else has ever proved that evolution by natural selection is the only—or even the most likely—explanation for how life on Earth evolved!”
Very good point. I have been writing a long essay on exactly this topic, to be posted in the blog in two weeks.
June 4, 2015 at 6:08 pm
J.J. Emerson
To be fair to your daughter, as I recall it, she was so busy doing excellent training and work in the lab, that there was scarcely time remaining to fit in similarly thorough training on informatics and statistics.
June 3, 2015 at 8:36 pm
pmelsted
This is the future of data-science. Even though there are still entries to be submitted, I’m pretty sure we’re not going to reject any sensible null hypothesis. There have been several analogies that explain the phenomena observed, that only one of the gene pairs has an accelerated rate of evolution.
Let me offer yet another one, that is a variation of the dice one presented above, but with more extreme parameters. Consider a million people, each buying two lottery tickets and each lottery ticket has a 1 in thousand probability of winning. Now we observe that 990 people won and out of those only one person had two winning tickets. We could look at those winners and say that the tickets are obviously coordinating because only one of the pairs is winning.
Focusing only on the winning tickets we might say that this is “striking” and in some sense it is natural to be “struck” by these numbers. However this would be an illusion, because once we focus only on the winners we are working in a conditional probability space. Humans are terrible with conditional probability our intuition is awful and we should never rely on it. I think my intuition is so-so in the full probability space, but this is most likely because I have been trained to distrust my intuition, even more so with any conditioning. We do this when we teach probability, tell students horror stories about fallacies of conditional probabilities. This is why we spend a whole lecture on the Monty Hall problem, not because we want to win the car (or goat if that’s what you’re into), but because we need to stop trusting our intuition.
We can also think of the original experiment by writing up a Bayesian network describing the two gene pairs and the derived indicator variable of whether the pair is accelerated.
+--------+ +------------------+ +--------+
| Gene 1 +---->+ Pair accelerated +<----+ Gene 2 |
+--------+ +------------------+ +--------+
Looking at this we have encoded the following assumptions, gene 1 and gene 2 are independent (i.e. whether they are accelerated), but once we observe the middle state, the two variables become dependent. The observation that the two variables are dependent in the conditional probability space does not imply that they are dependent in the full probability space.
This is one of the issues here, the authors were struck by something and didn’t distrust their intuition, write down the statistics and convince themselves that they were working with the right model. Moreover, comparing likelihoods between the two models (I’m deliberately not using the word probability here, because these are two distinct probability spaces), does not consider all alternative models of which there are infinitely many.
And I’m afraid this is the future of data-science, finding patterns in data that disappear once we view them through the lens of statistics.
June 4, 2015 at 10:28 am
Devin Scannell
Thanks Lior, Pavel and everyone for the great discussion. Thanks Manolis for investing the time and for being so cordial– Not all the comments here have met the bar of meaningful scientific discussion.
Please find below a further comment I wrote a few days ago. I debated posting it but given that Pavels students are reading, I decided it is best to have it out in the wild.
Before that however, Manolis, I find myself compelled to question your most recent comments.
1# – You say in your second bullet “Force et al. proposed an alternative model whereby both gene copies would be relieved of selection symmetrically“. I really don’t see where this point is intended in their paper. Do you mean reciprocally? For example, an ancestral gene with 9 subfunctions could give rise to a daughter within one 1 subfunction and another with 8. This would perfectly fit the subF model – reciprocal inactivation of functions – but would not be symmetrical at that level. Moreover, in the paper they talk extensively about (sub)functions, but they do not make any predictions about sequence evolution including in the section titled “Testing the DDC and classical models” (where they make 5 testable predictions).
2# – I make slightly more detailed points below but generally I find it very hard to see where you are getting the idea that the Ohno model uniquely predicts asymmetric evolutional. All the models you mention (bar gene conversion) are compatible with asymmetric evolution:
NeoF – Consistent with asymmetry (though it might apply to just a handful to AA sites so would not necessarily be easily observable)
SubF – Consistent with asymmetry (but does not make a strong prediction; see my previous comments or the example above of 1 vs 8 subfunctions)
Dosage – Consistent with asymmetry. Alan Drummond (who commented I believe) has shown that expression level explains 50% of the rate of protein evolution. Since very many of the duplicates are expressed at different levels (see my Genome Res. paper for one example) we expect quite different rates even for duplicates that both continue to perform the ancestral function.
Regardless of P-values, I cannot see how the analysis of rates can truly support the Ohno model.
——————————
Other comments:
Since Pavel’s students will be reading this, I’ll make one final contribution. Ian Holmes’ attempted to simplify the discussion into a disconnect between P-values and model comparisons. This is almost right. The problem – as Ian also points out – is that rates are not models (rather “nuisance parameters”). The models that we would like to test are neofunctionalization and subfunctionalization (others also possible) but they do not make clear (or even distinct) predictions about rates. SubF and other models are entirely consistent with asymmetric rates of evolution (see previous comments). Moreover, Ohno contributed a lot but he never substantiated that asymmetric rates of evolution indicate one member has adopted a novel function.
So, for the benefit of Pavel’s students, the problem here is not that no P-value was calculated, or that people disagree about how it _should_ be calculated. The problem is one cannot test a hypothesis without first identifying clear testable predictions. In this case, the analysis of evolutionary rates, cannot distinguish the models. P-values cannot rescue this problem.
The authors conclude: This strongly supports the model in which one of the paralogues retained an ancestral function while the other, relieved of this selective constraint, was free to evolve more rapidly1 [1 references the Ohno model]. The conclusion is contradicted by the (admittedly limited) experimental data we have from van Hoof (as I mentioned in a previous comment) and from Lauren Rusche (who I should have cited before) on the SIR2/HST1 pair (http://www.ncbi.nlm.nih.gov/pubmed/21690292) and also ORC1/SIR3 (http://www.ncbi.nlm.nih.gov/pubmed/20974972). All of these pairs have undergone subF (both duplicates retain ancestral functions) while also displaying sometimes great asymmetry in rates**.
Overall, we have a situation where the evidence proposed in favor of the Ohno model is not based on robust analysis and several experiments from different labs provide meaningful evidence for subfunctionalization. Further data could change the picture but it is premature to conclude that the Ohno model of neofunctionalization is important after the yeast WGD.
** The notable paper on GAL1/3 by Chis Hittinger does not fit either of the models getting attention here
July 7, 2015 at 10:52 pm
F. B. Pickett
Hi Devin, I appreciated your comment 1 above, writing the original theory on the chalkboards in Willamette and Klamath Hall at Oregon with Allan Force in 1993/4 before we sought Mike’s help on developing the math of the model I can confirm that we absolutely were not making claims about sequence divergence rates…we assumed that they would be all over the place early on and that the majority of pairs would quickly re-enter purifying selection and thus both genes would evolve slowly for a time as they became functionally more distinct. We tried to include some “what ifs” in the paper but did not make the odd claims folks are discussing above. Frankly Allan and I were baffled by the rate claims folks were making later in light of Van Hoof’s work, who we communicated with often in the old days…rates did not capture subfunctionalization data that we could detect. We assumed slow divergences would be a signal of successful subfunctionalization and subsequent purifying selection as each gene became necessary, either qualitatively or quantitatively (Arlin’s work and our later work discussed this) to the life of the organism….Allan and I would look at the slow evolvers as successful products of DDC.
Of course after preservation new alleles would continue to form, but we could not see how to disentangle alleles resulting from DDC early in the process from alleles arising later looking at extant genes, except through function testing ala Van Hoof. Over the years I have kind of given up on reminding folks that DDC happens quickly if it was involved in preservation of duplicates, nulls sweep duplicates away if DDC or neofunctionalization does not happen quickly, but that full resolution of partial redundancy might happen slowly or not at all depending on constraints and permissible mutation space…some of which could of course include the acquisition of neo functions as the genes explored their own mutational events in the long evolutionary history of each species. DDC was in our minds about initial preservation of duplicates, not about explaining the entire evolutionary history of extant genes, which seems to be how people are trying to use the model now…we assumed after preservation “mutation happens” and that many extant alleles/genes would have diverse sequence difference that held no signal regarding the preservation event..this again was why we were so energized by Van Hoof’s seminal and I have to say I think under appreciated function testing work.
The confounding effects of diverse sources of sequence divergence have off and on been pointed out by others, including the fact that diverse rates can be equally explained by contradictory models..Proulx 2012 Multiple Routes to Subfunctionalization is interesting here as are some of his other harder to find model work. Our later papers seem to get less play, and the “book chapter” (egads) we published in Wagner’s excellent Modularity from U of Chicago press also seems to get less attention, sequencing and post genomics stole the narrative about gene duplication in a truly bizarre fashion I hate to say. When you have a hammer every problem is a nail I suppose :-).
Anyway, your narrative is a concise and accurate representation of our work, NHGRI’s strange take on what computational biology should become over the last 15 years (I think we thought there would be a lot more theorists charting the terrain than analysts counting the grass 🙂 ) has spawned a generation of folks who assume very strange things about pre-genome work..and I am afraid are no longer doing a close reading of the original literature…our interpretation of Ohno was in no way dismissive, we had the highest respect for his work, our paper simply used his narrative as one example supporting neofunctionalization and one has to remember that his monograph was mostly a survey and review/philosophical treatise rather than an explicit précis of a model. Folks are putting a lot of meaning into Ohno’s turns of phrase because that is what he gave us, it was a statement of a problem and a proposed theory and course of future investigation…but they may be overweighting his statements to fit their own expectations, Allan and I would surely have been as guilty of this as anyone, and certainly if we misunderstood his work we would be the first to acknowledge this, we considered him an inspiration and a guiding spirit in our own thinking, he was outside the box before anyone else realized what the box was. In our defense I will say Lior’s excellent introduction is a simplification of the ideas of the DDC paper and our subsequent work…hopefully the community will rediscover this work before weighting it with too much of their own baggage, I mean this respectfully but I worry that web summaries are the starting point of too many model discussions that should be grounded in close reading of the original literature.
A side note to Arlin, cheers my friend, Vicky and I extensively referenced you in Seeing Double, Appreciating Genetic Redundancy in Nature Reviews Genetics some years ago…I share your frustrations, it is easy to vanish in the shadows if we are not generously acknowledged, your ideas, energy and inspirations at the early meetings were central to the ferment that DDC emerged from :-). I am really irritated that the centrality of your role in these ideas seems to be treated flippantly by others in the thread…read Arlin’s papers folks, good stuff, he is a pioneer intellect on the path you are all treading…has anyone asked him to chair any good sessions lately? Warmest regards, Bry.
June 4, 2015 at 12:40 pm
homolog.us
“van Hoof found no derived/novel function of SIR3 whatsoever!”
In the lab, which is the supposed natural environment of S. cer and K. lac, right? 🙂
June 4, 2015 at 2:16 pm
Michael Eisen
After my plea for Lander and Kellis to admit they were wrong, Eric emailed me to ask what I thought was wrong about his statement. I won’t post his email here, since he sent it to me personally, but I’m uncomfortable taking this conversation offline like that. So I attach my reply here.
——
Eric-
To cut to the chase, the statement you are referring to was born of my assumption that someone as smart and insightful as you can not possibly believe that the analysis in Manolis’ paper is right in any meaningful sense of the word, and hence frustration that you have nonetheless chosen to defend it on narrow technical grounds. I’ll provide specifics below, but there is more at stake here than the fate of a statement you made in a paper a decade ago.
Real progress in science requires that we constantly reexamine and hold up to scrutiny the work of our colleagues, especially when they have gained some traction, as this work has. Whatever you think of his style, Lior’s blog is one of the few places where this kind of scrutiny takes place in a public forum, and I find it invaluable. The discussion of the analysis from Manolis’ paper has been interesting, enlivening and instructive, and has engaged a large number of very bright people – science functioning like the Baconian ideal to which we all aspire.
So I hope you can appreciate why I found it disappointing that your and Manolis’ comments seemed to all but completely ignore this discussion – their purpose seemed not to explain or to discuss but rather to defend an analysis and conclusion that, based on comments on Lior’s blog and elsewhere, as well as a large body of additional evidence, are no longer defensible.
We all get things wrong sometimes – whether because we apply methods that are flawed or because our conclusions are shown by subsequent work to be incorrect (or both). But what distinguishes a scientist from a member of a debate club is the way we respond – whether we choose to defend our error or to learn from it. And, to be blunt, I found your and Manolis’s responses in this light to be wanting.
As for the specifics. Let me start by saying that I understand the way in which the “striking” assertion was made in the paper. Viewed narrowly in the context of the question and method used, the 95% number can be viewed as striking. However, I simply can not see how, in light of the points raised in the blog comments and elsewhere, one can come to any other conclusion than that the point is wrong in every meaningful sense of the word.
First of all, the analysis was poorly done. Applying an arbitrary cutoff to a series of quantitative data and then performing statistical analyses is intrinsically fraught and prone to giving misleading results. It naturally makes people worry about how the cutoffs were chosen. When the paper was originally published we discussed it in our journal club and concerns were immediately raised about this facet of the result, leading to one of my students reanalyzing it with more sophisticated methods and concluding that the result was not correct in even the narrow sense it which it was framed (this is discussed at length in the comments on the blog). In addition, analyzing only pairs in which at least one gene showed accelerated evolution was an odd choice whose effect was to make the result appear more striking that it actually was. I don’t think this was the right way to analyze the data – even in the context of a two-headed model comparison – and I find it hard to believe that you do either.
Second, the framing of the question and presentation of the result appeared more about getting a result than about revealing something about the underlying mechanisms of evolution following duplication. Even if you accept the result at face value, what you really show is that duplicated genes are not evolving at the same rate. If we stipulate that, one could argue, as you have done, that this analysis rejects a naive model of evolution following duplication. But in no way does rejecting this model do what you claim – that is provide “strong support for a specific model of evolution” or allow you “to distinguish ancestral and derived functions”. To do this you would have had to, at the minimum, have considered alternative explanations for the observation. As you can see, most of the blog comments revolve around the failure to have considered the most obvious alternative explanations for the data – especially the model in which genes are simply evolving independently – a possibility that fits the data very well. Thus the claim about the data supporting a specific model of evolution is wrong both in that the results don’t actual support the claim, and that there are other explanations for the result.
Finally, even if you stand by the analyses you published, I think it is more than clear from subsequent work that the overarching claim is simply wrong. Rather than defending the original analysis, shouldn’t this new data lead us to reexamine the analysis to understand why it was wrong?
I’m sure you do not agree with me, but I hope this makes it clear what I meant. Since it seems that you took some offense at my comment, let me also be clear that I was not expressing disdain – I think it is a natural instinct to defend one’s work – but rather disappointment that we missed an opportunity for America’s most prominent scientist and scientific mind to show young scientists how things should be done. But perhaps the moment has not yet passed.
Best wishes, as always.
-Mike
June 4, 2015 at 3:57 pm
homolog.us
……and let’s not forget that Lior Pachter accused Kellis of scientific fraud in a previous post (or rather a series of three posts).
https://liorpachter.wordpress.com/2014/02/12/why-i-read-the-network-nonsense-papers/
For old-fashioned scientists like me from the previous century, that is a fairly serious charge to make in a public forum. Unless we assume that Pachter makes such claims lightly and should be ignored, Lander (founder of Broad Institute) should have some responsibility to make sure it gets addressed to a level beyond calling Nature Genetics and replacing supplements.
It appears to me that Pachter’s current post is an ‘escalation of the issue’. Is he going to escalate to the Eli Broad level in a future post? 🙂
June 5, 2015 at 2:51 am
Eddie
you mean nature biotechnology?
June 5, 2015 at 10:40 am
winterschlaef3r
No, the opportunity has not passed yet. I am really looking forward to another statement by Eric Lander here — who is not only a great scientist but also a great teacher (I was one of his students in 7.00x)
June 5, 2015 at 8:11 am
homolog.us
Yes Eddie. Thanks for the correction.
June 6, 2015 at 12:22 am
Tatiana Seletskaia
Hello, I am one of Pavel’s students. I have PhD in physics meaning that I might be thinking a bit different from you, guys. Though, we use the same math constructions such as graph theory, path integrals, etc, nevertheless, the way we define systems and use concepts like space of the states, nodes, weight of edges, are different. Let me present my thoughts here on the subject. Please correct me if you see misconceptions.
The null hypothesis is the same as one given by few people above. It is independence hypothesis: After whole genome duplication the pairs of genes evolve toward protein function independently
Data: 457 gene pairs, in 76 pairs only one gene demonstrates accelerated evolution, 4 pairs of genes evolve in both pairs at the same rate
Testing: If relative acceleration is just a coincidence, the probability of 80 genes out of 914 to be simultaneously accelerated is P = pow(80/914, 2) = 0.007661. A random variable X can have two values either be dependent or independent, therefore, it is described by binomial distribution. Binomial cdf for 457 trials and X<=4 is p = 0.73 that indicates that in the given statistical ensemble 4 pairs might be enough to conclude that accelerated evolution in the pairs was independent.
So far, the whole discussion is concentrated on calculation of a p-value. But I think that in genome evolution not only the speed of amino acid replacement might be important. The authors mentioned that positions of the accelerated codons also tell about asymmetry of genome functionalization that was predicted by Ohno. This statement distracts me from getting to a final conclusion. Bio-informatics appears to me to be an empirical science and one can judge whether number of independently accelerated genes or codon coordination is more important for neo-functionalization model only after having actual working experience in the field.
BONUS: Science and Nature are popular science journals. They advertise scientific work. It is a problem of scientific society, not of the journals that they have extremely high ranks and publishing a paper there is a matter of success.
I am looking forward to see the arguments of Prof. Pachter.
June 6, 2015 at 2:18 pm
Pavel Pevzner
I thought some readers of this blog may find this Coursera post relevant to the ongoing discussion.
Dear students, I noticed that many of you are still working on HMMs but I know some of you are already learning about the P-value prize. In view of the upcoming imminent release of the P-value prize tomorrow, I wanted to provide a historical background on an elephant in the room that some contestants (and even the moderator) may have missed. Particularly, wrt the phrase in the Rules:
“…explain in your own words how you think the paper was accepted to Nature without the authors having to justify their use of the word “strikingly” for a MAIN result of the paper…”
I have to confess that I never thought that “Strikingly” and the related few paragraphs in KBL represent the MAIN result of KBL. The lion’s share of KBL presents an algorithm for constructing synteny blocks (remember our own synteny block construction algorithm from Lesson 5 :-)) and has nothing to do with “Strikingly.” And “Strikingly” has nothing to do with WGD – the authors could have made the same point about “Strikingly” in a paper arguing AGAINST WGD! Indeed, their arguments apply to any set of yeast paralogs, does not matter whether WGD is real or not.
This comment brings us to the MAIN point of KBL. To understand the important role the KBL played, one can look at the fierce “to WGD or not to WGD” debate in the 1990s that KBL finally resolved in 2004. But has KBL ever computed the p-value for WGD??? Why such an interest in computing the p-value for a MINOR conclusion of KBL and no interest whatsoever in computing the p-value for the MAIN result?
The description of the p-value prize starts from:
“The authors identified 457 duplicated gene pairs that arose by WHOLE GENOME DUPLICATION in yeast.”
Presumably, if Dr. Pachter asks people to compute the p-value of “Strikingly,” he believes that WGD indeed took place. Why Dr. Pachter (like myself) has fallen into this trap without computing the p-value of WGD first? Should we ask him to announce a pre-sequel to the P-value prize and to compute the P-value of WGD before computing the P-value for “Strikingly”? Maybe our own Erica, Miguel, and Tatiana (who have already made some progress wrt KBL) will even have a chance to win it!
But maybe I am wrong – maybe Dr. Pachter does not really believe in WGD. I am curious to learn what he thinks on this matter before I present another piece of fascinating historical background on KBL. I am also curious to learn how many readers of Dr. Pachter’s blog think that WGD has been proven beyond reasonable doubt.
June 6, 2015 at 5:30 pm
More than 3rd reviewer
I largely agree with Pavel that the rate asymmetry was not the take-home message of the KBL paper. Although Wolfe and Shields (1997) presented strong evidence for a WGD, this paper really settled the matter.
June 6, 2015 at 2:49 pm
Erik van Nimwegen
Dear Lior,
Here’s my entry:
Imagine a statistician that knows nothing about the problem at hand or the way the data is analyzed. All this statistician knows is that a renowned scientist has told him/her that, when genes duplicate, this may lead their evolutionary rates to either
A) Stay the same
B) Accelerate for one but not the other (asymmetric acceleration)
C) Accelerate for both (symmetric acceleration).
In addition, the statistician is told that there is a debate whether case B or case C is more common. The statistician is now told that a careful analysis has led to a data-set in which there were 381 cases A, 72 cases B, and 4 cases C.
They are asked: Is this strong evidence that B is more common than C, or may they be equally common?
The statistician now reasons as follows:
Because we only care about the relative occurrence of cases B and C, we can discard all cases A.
The hypothesis we want to test is whether both cases are equally likely, i.e. p(case B) = p(case C) = 1/2
Under this hypothesis, and a single-tailed test, the probability to get only 4 of 76 pairs is:
p = sum_{k=0}^4 Binomial[76,k] (1/2)^76 = 1.8 * 10^(-17)
Case C is really under-represented!
Of course one can do a million variants of this.
The problem, in my opinion, is not the statistics. The problem is pretending that we can precisely tell the cases A, B, and C apart based on our data. Once one does that, it is easy to lose sight of the fact that 80/(2*457) is very close to 8/80.
June 7, 2015 at 10:25 am
Lior Pachter
This entry was sent to me via email:
Hi Dr. Pachter,
I was intrigued by your Pachter’s p-value prize. What do you think of the following:
Where the expected value for Accelerated:Paralog A+B = (40/457)^2*457=3.5.
Chi-square value= 0.072
Df=1
p-value=0.79
Cool challenge!
Best regards,
Tev Stachniak
Tevye Stachniak
Postdoctoral Research Associate
F.Hoffman-La Roche AG
Discovery Neuroscience
Bld. 70/406
Grenzacherstrasse 124
Basel 4051, Switzerland
June 7, 2015 at 11:14 am
Pinko Punko
Hi Lior,
When you announce the results, I wonder if you might also publish the page hits for this entry, because I am amazed and pleased by how widely this post is being discussed. I suspect there are quite a number of lurkers like myself who value it greatly.
June 8, 2015 at 5:54 am
Lior Pachter
This blog post has been viewed >24,000 times since I posted it on May 26th, and the homepage of the blog (on which this post has appeared first) has been viewed an additional >46,000 times since that time. That is a total of >70,000 views so far. The blog as a whole surpassed 1 million views on Saturday. It was launched on August 19th, 2013.
June 7, 2015 at 8:59 pm
reader
I agree with the formulation put forward by oz on May 26, 2015 at 5:55 am. However there is one correction I’d like to offer, as well as a motivation for this “independent” model as a null model here.
First, upon reading the M&M and taking a cursory glance at the Supplementary Tables from Kellis, Birren and Lander, 2004, we find that:
– 7 paralogs were excluded from this analysis with a reasonable motivation (data in S9_Trees/Duplicate_Pairs.xls, “All Data” tab includes just 450 pairs).
– 7 of the remaining pairs include “branch lengths” that are negative. It is unclear how to handle this issue, though it appears that these were excluded. I’m not sure how to interpret these pairs but perhaps the authors could chime in.
This leaves N=443 pairs, not N=457, and with the same analysis as oz, this makes a slight correction to the p-value to p=0.7212 (his was p=0.743).
Contra the point by Kellis, even if the “independent evolution” model is bogus as he suggests (convincingly), this does not make this an unreasonable null model for this analysis here. Quite the opposite — the fact that the model fails to exclude this hypothesis shows the weakness of this analytical approach, which could be caused by numerous other factors.
June 7, 2015 at 9:56 pm
Max Shen
As an undergraduate researcher in Pevzner’s lab that will be entering a bioinformatics Ph.D. program in the fall, following these discussions has been an invaluable experience! It’s hard to see something similar benefiting students like me just a generation ago. The discussion got me thinking a lot about appropriate null hypotheses and model comparison tests.
There’s not much new that I can add. It is clear from the math performed by many others that under a null hypothesis of independent evolution, KBL’s results are not impressive. However, it is also clear that under KBL’s model comparison paradigm, the results are indeed “striking”.
The conclusion that appears to me is that KBL’s paper is largely self-consistent and provides data that support a “striking” argument against subfunctionalization, though for the sake of more complete science, perhaps it would have been appropriate to mention the alternate null hypotheses that is the first thought to many others, independent evolution, and reasons (as Kellis has provided above) to reject working with that null hypothesis.
I believe the unsaid conclusion can be described as: “The model comparison test performed on the data supports neofunctionalization over subfunctionalization. The data are insufficient to differentiate between independent evolution and neofunctionalization, but we reject the independent evolution hypothesis since duplicated genes share function, etc… As a result, we conclude that neofunctionalization is supported.”
It may then suggest further papers/experiments to test the idea that the independent evolution model is naturally inappropriate.
June 8, 2015 at 1:49 am
Michael Eisen
Manolis and Eric, would you guys be willing to post the original reviews from Nature of this paper?
June 8, 2015 at 12:05 pm
Lior Pachter
I was asked to post the following comments by someone who wishes to remain anonymous:
=========================================================
1. Systematically absent gene subsets. There are at least 551 documented WGD pairs in S. cerevisiae — about 100 pairs more than the Kellis dataset. The missing (“hard to find”) ones are – of course – systematically biased towards fast evolving genes (See supplemental http://genome.cshlp.org/content/15/10/1456.long ). Gene pairs where both members are “accelerated” are most likely to be systematically depleted form the dataset creating a moderately serious ascertainment bias. On the upside, it is tempting to criticize KBL as an analysis of outliers but this error helps mitigate that.
2. A P-value not inflated by trivial factors would be more “striking”. Since expression level “trivially” explains ~50% of evolutionary rates in yeast ( http://www.ncbi.nlm.nih.gov/pubmed/16237209 ), substitutions due to expression differences would ideally be removed. The paper cited is from ’05 but in hindsight I think a “good faith” effort would be important unless one was interested in expression divergence also (which would be very welcome overall but is not where the conversation is focusing).
3. The framing as accelerated or not is obviously a major sticking point. Erik’s point is the main one but I’ll add that if one looked at a very short branch immediately after WGD, many more duplicate pairs would qualify as “accelerated”. In addition, both members of pairs would also qualify as accelerated vs an outgroup / suitable control. There is an important time dependence to this analysis in addition to sensitivity to the “cut off” for acceleration. (Why is nobody using counts of substitutions btw instead of rates?)
June 8, 2015 at 8:28 pm
D. Allan Drummond
When my colleagues and I read KBL back in 2004, we were–like many others, clearly–bothered by the “striking” claim. Our reasoning was a bit different and has been hinted at above: since 2001, when Pal, Papp & Hurst published the terrific little “Highly expressed genes in yeast evolve slowly” (http://www.ncbi.nlm.nih.gov/pmc/articles/PMC1461684/), mRNA levels had been known to be correlates of, and perhaps causes of, (relative) evolutionary rates.
To us, that meant that the null of independent evolutionary rates was a non-starter. Wrong model, unininterpretable P-value. Moreover, any claims about asymmetry would have to model in relative expression levels, which at that time had been measured genome-wide by several groups; we quickly showed that the higher-expressed paralog evolved slower most of the time. Finally, I did a little analysis showing that the asymmetric evolutionary rates persisted for roughly 100 million years after the WGD, which, while hardly a conclusive result, did not seem a plausible consequence of neofunctionalization.
With my colleagues (hazy memories here but Claus Wilke for certain, and I believe Jesse Bloom and Chris Adami), I wrote up a Brief Communications Arising to Nature making these points. It was swiftly rejected. I cannot find the notice, but remember that it stated that the conclusions we criticized were not sufficiently central to the manuscript. I remember this because I was pretty upset, in that indignant-young-graduate-student way — if the claim was prominently featured in the abstract, and the title included “evolutionary analysis,” how was this not central? But then I could not stop thinking about the problem.
That rejection and subsequent failure to stop thinking led to our 2005 paper “Why highly expressed proteins evolve slowly” (http://www.ncbi.nlm.nih.gov/pmc/articles/PMC1242296/), where the bit sent to Nature became a section of the paper (“Functional Divergence of Gene Duplicates and Evolutionary Rate”). That paper, in turn, became the core of my doctoral thesis. And so the KBL result is forever special to me, even though I have no idea how to compute a plausible P-value for it.
June 9, 2015 at 5:39 pm
Mike Rust
“I will award $100/p
to the person who can best justify a reasonable null model, together with a p-value (p)…”
I feel that it is my duty to warn the scientific community about the hazards of promising cash prizes like this. Since p is uniformly distributed under the null hypothesis, even when no effect is present, the expectation value of how much money you’ll have to pay out is infinite!
August 19, 2015 at 3:39 pm
Anon
An excellent discussion. Thanks for this Lior. Although I must say it’s a bit ironic that you cite the Lan/Pritchard papers, which contains the following statement:
“Surprisingly, many gene pairs instead show an unexpected asymmetric pattern of gene expression, in which one gene has consistently higher expression.”
Seemingly the only evidence I can find that this is “surprising” result is that 36.7% of paralog pairs have asymmetric patterns of expression compared to 10.7% of potentially sub-/neofunctionalized pairs. A 3-fold change seems impressive, but I see no mention of a null model, which seemingly puts it in same category as the “95% of all pairs” category you seemed to have an issue with in the Kellis paper. Perhaps a P-value prize Part 2 is necessary ;).
August 20, 2015 at 6:28 am
F. Bryan Pickett
Actually I have always puzzled over these types of statements, in the original model we suggested that asymmetric expression could be an example of quantitative subfunctionalization, a point we returned to often in later work as well..along loss of what we called Minimal Information Building Blocks in Gunter Wagner’s book Modularity..i.e. functional domains in proteins/alternative splice sites in mRNA etc. etc. that would lead to subfunctionalization that cold then be coupled to either qualitative or quantitative changes in expression which would have nothing to do with the original preservation event..extant states of expression help us form hypotheses, but functional test with unduplicated ortho/paralogs seemed to us to be the only real way to test these hypotheses…more expression studies just would generate more hypotheses about the evolutionary outcomes, not really test them ..We never focused only on divergence in transcription, that was just one case, granted an easy one for “high throughput science” to explore but we always cautioned folks to not look for their keys only under the streetlight….also one has to remember that expression states of extant genes may have nothing to do with the events that protected the duplicates from psuedogeny…a point we also have made repeatedly…original papers anyone?… :-). We assumed that evolution would continue to happen after preservation…that old clock keeps ticking :-). Extant genes capture their entire evolutionary history, not just the events that led to preservation.
Cheers
Bry
December 18, 2015 at 3:09 pm
acerase77
Manolis is right! leave him alone! 😉